Given numbers a, b, and c, we are familiar since elementary grades that a(b+c) = ab + ac. This is what we call the distributive property of multiplication over addition. From commutative property, we also know that xy = yx; therefore, (b + c)a = a(b+c).
Knowing this property, we can do a lot of mathematical operations. This property is enough for us to discover many strategies in algebraic manipluations. For example, we do not need to memorize FOIL (First-Outside-Inside-Last) , one of the strategies that our teachers have taught us before when multiplying two binomials.
If we know the distributive property, we should know that in the operation (a + b)(x + y), we should first multiply a(x + y), multiply b(x + y), and then add both terms giving us a(x + y) + b(x +y) which is equal to ax + ay + bx + by. If we have solved this, we can definitely solve (a + b)(x + y + z) and also (a + b + c)(x + y + z).
We can also see that the distributive property works for multiplication, and is actually the idea behind multiplication of real numbers. For example, in the operation 23 times 45, we use the distributive property to multiply the digits. First, we multiply 5(20 + 3) and then we multiply 40(20 + 3) and then add them both. It is also the same as (20 + 3)(40 + 5) = 20(40) + (20)(5) + 3(40) + 3(5) = 1035.
Another example on how to multiply algebraic expressions is shown below. Notice the similarity of both methods, and how it can be extended to multiplying numbers with more than two digits and algebraic expressions with more than two terms.
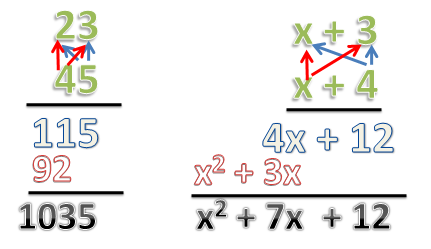
For greater number of terms, the box method might be of help. If we want to multiply x3 + 3x2 + x – 1 and 4x3 – 2x2 + 3x + 5, we can still use the strategies that we have done above, but placing it in a table as shown below might be more convenient.
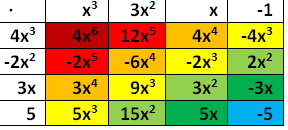
In the table, expressions in cells with the same colors have similar terms and therefore can be added.
On a final note, teaching strategies to students such as short cuts and mnemonics are not quite advantageous because we are depriving them of discovering these strategies on their own. After all, that’s what mathematics is all about. Finding the shortest path; finding the most elegant solution. If we as teachers find it for them, then we leave them with nothing to do.
Related Articles
Stumble It!
I’d never really thought about long multiplication as an example of distributivity – I just took as true in primary school (when I didn’t know better) and haven’t really thought about it since.
.
It’s also interesting to notice that powers distribute over multiplication ie)
Since multiplication of integers is repeated addition and raising to an integral power is repeated multiplication this makes sense.
I am glad I am beginning to see the connection now, many years after graduating college. What is truly amazing is we can delve deeper even in the simplest concepts.
Thanks for reminding me of some factoring problems I had considered 2 years ago. Would you know where to study the technique(s) of factoring the polynomials that are a result of two linear or quadratic trinomials being multiplied.
Can this be easily factored? 6x^2+11xy+24y+2x-10y^2 -8. Distributive in reverse!
[...] The Distributive Property [...]
[...] The Distributive Property [...]