The Definition of “Undefined”
In learning mathematics, we often encounter terms that are not always clear. Example of such term is the word undefined. What do we mean by undefined?
The word undefined may slightly differ in meaning depending on the context. In plain language, it means something which has no sensible meaning. For instance, during the time when the negative numbers were not yet invented, the numerical expression 5 – 8 has no meaning. In our time, we can say that 5 – 8 is undefined in the set of positive integers.
Below are some examples of the different contexts where the different meanings of “undefined” can be drawn.
Numbers
Square Root of Negative Numbers. The is undefined in the set of real numbers. This means that no real number exists that when multiply it by itself, the product is equal to -1. Note, however, that some operations may be undefined under some sets, but defined in other sets. We know from high school mathematics that square root of – 1 equals i in the set of complex numbers.
Algebra
Division by 0. Since we do not know the answer if a number divided by 0, let us examine the quotient of numbers when divided by numbers close to 0. To make it simple, let us try 1/0.
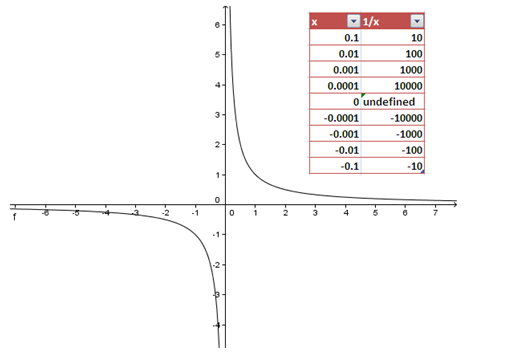
Figure 1 – The value of the 1/x as x approaches 0.
As we can see, as x approaches 0 from the right, the quotient of 1/x is getting larger and larger. On the other hand, as x approaches 0 from the left, 1/x is getting smaller and smaller. As a consequence, there is no single number that 1/x approaches as x approaches 0. Therefore we can say that 1/0 is undefined.
Geometry
Intersection of two lines. In Euclidean Geometry, if we talk about the intersection of two lines, we can have three cases: intersecting lines have one intersection, coinciding lines have infinitely many intersections, and parallel lines have no intersection.
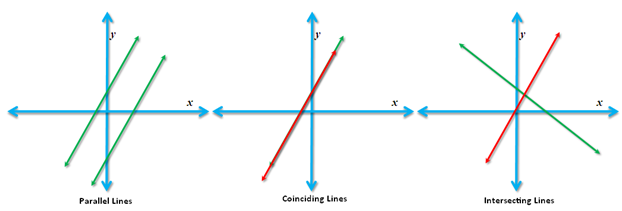
Figure 2 – The three cases, in terms of intersection, two lines can be places on a plane.
We can say that if two lines are parallel, no intersection exists. Algebraically, the solution to the system of equations of the two lines is their intersection. Hence, the solution of the two systems of linear equations of parallel lines as graphs is undefined.
Matrices
Matrices with Different Sizes. If A is a 2 by 2 matrix and B is a 3 x 3 matrix, then A + B has no meaning since five of the entries of matrix B have no corresponding entries in matrix A. We can say that the sum of matrix A and matrix B is not well-defined.
Sets
Intersections of Sets. If E is the set of even integers and O be the set of odd inteers, then there is no common value to both sets.

Figure 3 – The Venn Diagram of the intersection of even and odd numbers.
In set theory, we call the common values the intersection, and in this example, the intersection is the empty set. As a consequence, we can say that the intersection of set E and O is undefined.
***
Although the word “undefined” has different meanings depending on the context, by now, you would have realized that the phrases “does not exist”, “without sensible meaning” and “cannot be determined” are somewhat synonymous to it. If the result of an operation yields no value at all (note that 0 is a value and is not the same to no value), then it is more likely that it is undefined.