Sets: A Gentle Introduction

There are people who are fond of buying things in sets. For example, a pen collector may collect pens of different colors.   Other people are obsessed with brands.   For instance, Apple fans may buy the following an iPhone, iPod, iPad, and an iMac. If you are fond of reading Dan Brown, you probably have read or own some of the following books: The Lost Symbol, Deception Point, Digital Fortress, and The Da Vinci Code, and others.

In mathematics, a set is not very different.  A set is can be described as a collection of objects with common characteristics. These objects are called elements. Given a set and an object, it is clear if the object is an element of a set or not.  If we let D be a set of Dan Brown novels, then D = { The Lost Symbol, Deception Point, Digital Fortress, The Da Vinci Code}. Also, if we let V be the set of vowel letters in the English alphabet, then V = {a, e, i, o, u}, and if we let R be the set of polygons whose number sides is less than 9, then the set would include the polygons in the figure below.

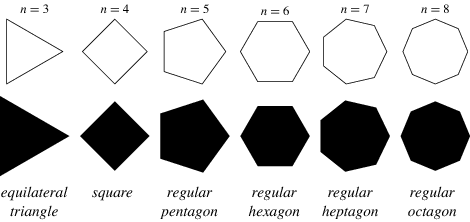
As we can observe, sets maybe described or listed. The vowel letters in the English alphabet is a description of the list {a, e, i, o, u} . It can also be noted when listing that the elements of the sets, by convention, they are enclosed with curly brackets and are separated by a commas as shown above.

As we have also mentioned, we can easily see if an object is a member of the set or not.  We are sure that a is a member of V. We use the symbol to denote membership in a set. Hence, we can write a is an element of V (or is a member of V) as . On the contrary, b is not an element of V and write .

Sets can be finite or infinite. Finite sets are sets whose elements can be counted, otherwise infinite sets.  The set of counting numbers N = {1, 2, 3, 4, … } is an infinite set.  The … symbol denotes that the list continues indefinitely. The number of elements in a set is called its cardinality. Hence, the cardinality of V is 5 and the cardinality of D is 4.