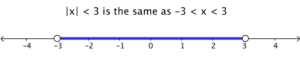Understanding the Meaning of Absolute Value
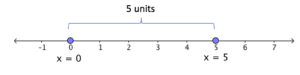
One important concept in algebra that we learn is the distance between two points on the number line. In particular, we study the distance of a point that corresponds to a number to the point that corresponds to 0. In the following figure, the point (or circle) on the left represents 0, while the point on the right represents 5. To simplify our language, we will use coordinates to refer to its corresponding point on the number line. For instance, we will use -8 to refer to the point that corresponds to -8.
Looking at the number line, it is easy to see that 5 is 5 units away from 0 and that -8 is 8 units away from 0. We can also see that 0 is 0 units away from 0. The distance of a number from 0 on the number line is called its absolute value. Hence, the absolute value of 5 is equal to 5, the absolute value of -8 is equal to 8, and the absolute value of 0 is equal to 0.
The Symbol for Absolute Value
We use vertical bars to denote absolute value. The absolute value of 5 can be written as |5|, the absolute value of -8 can be written as |-8|, and the absolute value of 0 can be written as |0|. From the discussion above, it follows that
|5| = 5
|-8| = 8
|0| = 0.
From the three equations, we can see that the absolute value of any number is greater than or equal to 0. After all, there is no such thing as a negative distance. So, for any real number x, we have |x| ≥ 0.
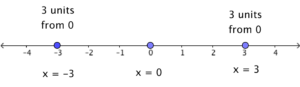
What do we mean by |x| = 3?
The absolute value of a number is its distance from 0, so what is the value of x if its absolute value is equal to 3? Equivalently, what numbers are 3 units away from 0? As we can see on the number line, there are two of such numbers: 3 and -3.
So, if |x| = 3, then x = 3 or x = -3. Similarly, if |x| = 2.4, then x = 2.4 or x = -2.4. Clearly, for a positive k, |x| = k means that x = k or x = -k. We can also write that if |x| = k, then x = ± k.
What do we mean by |x| < 3?
The absolute value of a number is its distance from 0, so|x| < 3 refers to points which are less than 3 units away from 0. Some of such points on the right of 0 have coordinates 1, 1.3, 2.9, and so on. Also, some of such points on the left of 0 have coordinates -0.5, -1.4, -2.1, and so on. This means that |x| < 3 refers to numbers between -3 and 3 not including -3 and 3. That is, |x| < 3 is the same as -3 < x < 3 or (-3,3) in interval notation. The graph of this inequality is shown in the following figure.
In general, for a positive number k, |x| < k means that -k < x < k or (-k, k) What do we mean by |x| > 3?
The absolute value of a number is its distance from 0, so |x| > 3 refers to points which are more than 3 units away from 0. On the right of 0, this includes points with coordinates 3.1, 4.5, 6, 8, 100 and so on or equivalently real numbers that are greater than 3. On the left of 0, this includes points with coordinates -3.1, -4, -50, -100 and so on or equivalently all real numbers that are less than -3. In effect, |x| > 3 means that x > 3 or x < -3 or (-∞,-3) ∪(3, ∞) in interval notation. The graph of this inequality is shown in the following figure.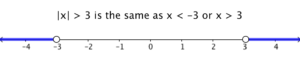
In general, for a positive k, |x| > k means that x > k or x < -k or (-∞,-k) ∪(k, -∞) in interval notation
Summary
From the discussion above we have learned that
For any real number x,|x| ≥ 0.
If |x| = k, where k is a positive real number, then x = k or x = -k.
If |x| < k, where k is a positive real number, then – k < x < k If |x| > k, where k is a positive real number, then x < -k or x > k.
In the next post, we will use these concepts to solve absolute value equations and inequalities.