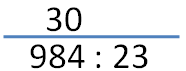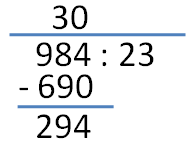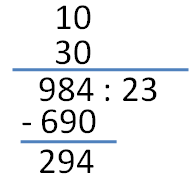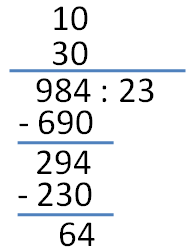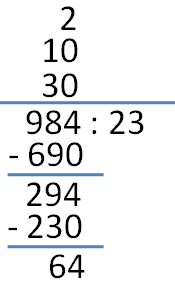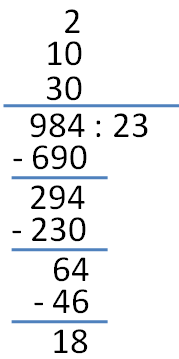A Different Way to Perform Division
All of us are familiar with the standard division method. The standard algorithm requires us to divide the digits with highest place values and get the largest possible quotient. For example, in dividing 984 by 23, we have to divide 98 by 23 which gives a quotient of 4.
The method that I am going to discuss below does not separate the digits. It lets you repeatedly divide and allows you to choose a more convenient quotient. Below are the steps of this method. We use 984 divided by 23 as example.
1. Write the dividend and the divisor separated by a colon and then draw a line above the numbers as shown.
2. First, we divide 984 by 23. Well, we don’t have to find the actual quotient. Maybe 30 is easier, so we choose 30. We write 30 above the line aligned to the place values of the dividend.
3. Next, we multiply 30 by 23. This gives us 690. Next, we subtract 690 from 984 which results to 294.
4. Next, we divide 294 by 23. The easiest quotient is 10. We write 10 above 30.
5. Next, we multiply 10 by 23. This gives us 230. We subtract 230 from 294 to give us 64.
6. Next, we divide 64 by 23. The quotient is 2. We write 2 above 10.
7. Lastly, we multiply 2 by 23 which results to 46. Then, we subtract the product from 64. The difference is 18.
Since 18 is less than 23, this means that this is the last step in the division. This also means that 18 is the remainder 984 divided by 23.
8. To get the final answer, we add the numbers above the line: 30 + 10 + 2 = 42.
This means that the quotient of is 984 divided by 23 is 42 remainder 18.
The division method discussed above is said to have originated from Germany. Although it is longer than the standard algorithm, it is less prone to mistakes. In this method, we can always choose a more convenient quotient and thus easier than the standard method.
Reference: Study with Your Friends Mathematics for Elementary School, Grade 4 Volume 1, Gakkohtosho