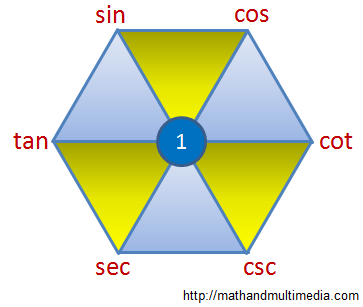
The Trigonometric Ratio Hexagon

January 5, 2013 GB High School Mathematics, High School Trigonometry

I found a book this morning containing a hexagonal figure of trigonometric ratios. It reminded me of the mnemonics I created when I was still in high school in order to remember the formulas during exams. Unlike in other countries, we were not allowed to have formula sheets during exams, so we have to memorize them all.

In the figure, any trigonometric ratio is a product of its immediate neighbors. Therefore,

$\sin \theta = \tan \theta cos \theta$ ****** $\cos \theta = \sin \theta \cot\theta$

$\cot \theta = \cos \theta \csc \theta$ ****** $\tan \theta = \sin \theta \sec \theta$

$\sec \theta = \tan \theta \csc \theta$ ****** $\csc \theta = \sec \theta \cot \theta$ .

In addition, the trigonometric rations at the opposite of the same end of the diagonals are reciprocal of each other. So,

$\sec \theta = \displaystyle\frac{1}{\cos \theta}$

$\csc\theta = \displaystyle\frac{1}{\sin\theta}$

$\cot \theta = \displaystyle\frac{1}{\tan \theta}$ .

For students, although, it is better to memorize these formulas, the more important thing is to be able to understand these relationship and derivation and proofs. That way, in case you forget them, you can still derive them by yourself.

The Trigonometric Ratio Hexagon

Leave a ReplyCancel reply