The Inscribed Angle Theorem and Its Applications
An inscribed angle is an angle formed by two chords of a circle with the vertex on its circumference. In the first circle in Figure 1, segments AB and AC are chords of a circle and the vertex A is on its circumference. Hence, angle A is an inscribed angle. In the second circle in Figure 1, angle Q is also an inscribed angle.
Angles formed by the two radii of a circle are called central angles. The vertex of a central angle is on the center of the circle. In the Figure 1 below, angles BOC and SOT are central angles.
The arc determined by the endpoints of two chords or two radii, and is opposite of the angle, is called the intercepted arc. In the first circle in Figure 1, arc BC, denoted by the red curve, is the intercepted arc of angle BAC (or angle BOC). Similarly, in the second circle, arc ST denoted by the green curve, is the intercepted arc of the central angle SOT. Saying the other way around, angle BAC is the subtended angle of arc BC and and angle SOT is the subtended angle of arc ST.
The Inscribed Angle Theorem
In this article, we are going to discuss the relationship between an inscribed angle and a central angle (I have created a GeoGebra applet about it) having the same intercepted arc. This is shown in the first circle in Figure 1. Angle BAC and angle BOC have the same intercepted arc BC. Therefore, if a central and an inscribed angle have the same intercepted arc, the measure of that central angle is twice that of the measure of the inscribed angle.

- Figure 1 – Inscribed angles, central angles and their intercepted arcs.
One strategy to solve a problem in geometry is to sometimes draw lines from one point to another. These lines drawn are called auxiliary lines.
Consider the first circle in Figure 1. Let us draw a diameter of a circle with A as endpoint, and let D be the endpoint opposite of A as shown in Figure 2. If we let the measure of , then,
since COA is an isosceles triangle. Since the angle sum of a triangle is equal to 180 degrees,
degrees. This implies that angle
and angle
. This is the same with triangle AOB as shown in the Figure 2. Therefore, if angle
, then the central
. Therefore, the measure of angle BOC is twice the measure of angle BAC.

- Figure 2 – The Proof of the Inscribed Angle Theorem
Exercise: In figure 2, prove that if C is on the circle and is between points B and D, the inscribed angle BAC is half that of central angle BOC .
We now baptize our new theorem, and we will call it the Inscribed Angle Theorem.
Theorem: If an inscribed angle and a central angle has the same intercepted arc, then the measure of the inscribed angle is half that of the measure of the central angle.
Thales’ Theorem and Cyclic Quadrilateral
The Greek philosopher, Thales, was first to prove – or at least, the proof was attributed to him – that the inscribed angles in a semi-circle, where the endpoints of the chords are at the endpoints of the diameter, measures 90 degrees. This will follow from the inscribed angle theorem since the angle containing the diameter is a straight angle and measures 180 degrees. The measure of inscribed angle C is half that of the central angle and therefore equals 90 degrees.
We can also use the strategy we used earlier by drawing an auxiliary line CD, where CD is a radius of a circle. In Figure 3 (second figure), if we let , then
since ADC is an isosceles triangle . This is also the same with BCD. If
, then
. By the angle sum theorem, the sum of the interior angles of a triangle is 180 degrees. Hence,
degrees. This means that
degrees. Dividing both sides of the equation, we have
degrees. As we can see,
is the measure of angle BCA. Therefore, the angle measure of an inscribed angle with its endpoints on both ends of the diameter is 90 degrees.

- Figure 3 – Angle C Inscribed in a semi-circle
The consequence of the theorems above is the theorem that the opposite angle of a cyclic quadrilateral always equals to 180 degrees. A cyclic quadrilateral is a quadrilateral whose vertices are on the circumference of the circle. In Figure 4, ADBC is a quadrilateral.
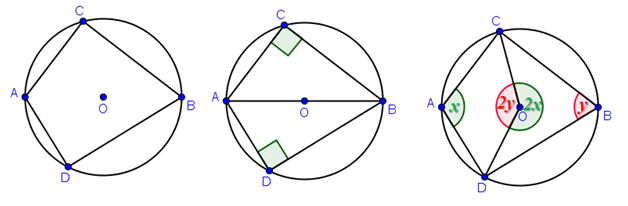
- Figure 4 – Proof that the opposite angles of a cyclic quadrilateral is 180 degrees.
In Figure 4, angle D and angle C are inscribed angles and both of chord endpoints at the diameter. Hence, their intercepted arcs are both semicircle (second figure). Therefore, both of them measure 90 degrees. The sum of their measure of course is 180 degrees. Now it follows that the sum of angle CAD and angle CBD add up to 180 degrees.
In the third circle (Figure 4), angle A and angle B do not intercept a semicircle. However, it is clear that 2x + 2y is the entire rotation around the circle which is equal to 360 degrees. Hence, x + y, which is the sum of the measures of the opposite angles A and B, equals 180 degrees.
Angle Sum and the Inscribed Angle Theorem
In the Parallel Lines and Transversals posts, we discussed and proved that the sum of the measures of the interior angles of a triangle is 180 degrees. This can also be shown using the inscribed angle theorem.
To prove the angle sum theorem, we are going to use the fact that given any triangle, that triangle can be inscribed in a circle (Can you see why?).
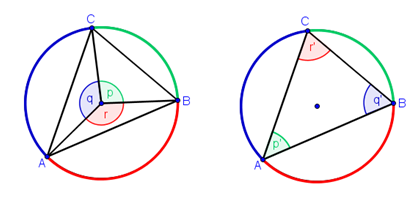
- Figure 5 – The Angle Sum Theorem via Inscribed Angle Theorem
Consider triangle ABC shown in Figure 5. To make the drawing easier to interpret, I have separated the drawing by showing the central angles , and the inscribed angles
and
. Note that
and
have the same intercepted arc, hence
. From the figure above, it is clear that
and
.
Since, degrees,
degrees. Hence, the angle sum of a triangle is 180 degrees.