Parallel Lines and Transversals
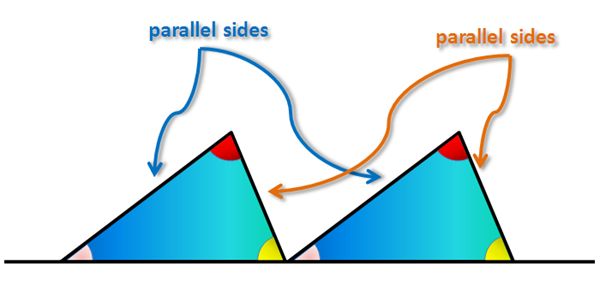
Given a triangle and a line segment, let us place the triangle such that one of its side and the line segment coincide. Next, we replicate the triangle and slide to the right hand side such that two of their vertices meet as shown in Figure 1.
The angles with the same color are basically the same angle, so we will call them corresponding angles. The sides which are parallel are also the same side, so we will call them corresponding sides.
What can you say about their corresponding angles? Their corresponding sides?
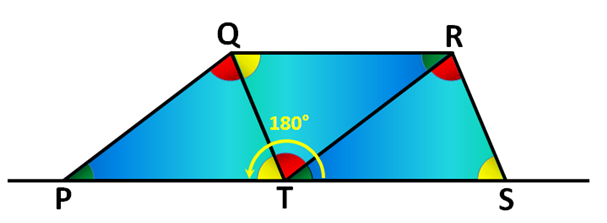
Next, we replicate one of the triangles, rotate it and place it between the two triangles as shown in Figure 2. Click here to rotate the triangles using GeoGebra. In the figure, we can observe and deduce the following:
- The measure of the three adjacent angles in T is half the circle and is therefore 180 degrees. This implies that the sum of the interior angles of triangle PQT is also 180 degrees, since they are the sum of the three adjacent angles in T.
- PQRT and QRST are parallelograms. (Explain why the opposite sides are parallel).
- The opposite angles of parallelogram are congruent, and their opposite sides are also congruent. (Explain why).
- We also observe that the sum of the consecutive angles of a parallelogram is 180 degrees. For example, the sum of angle PQR and angle QRT is 180 degrees.
- The interior angles of a parallelogram consists of 2 green angles, 2 yellow angles and 2 red angles, which means that the angle sum of the interior angles of a parallelogram is twice 180 or 360 degrees.
- PQRS is a trapezoid and the sum of its interior angles is also 360 degrees. (Explain why QR and PS are parallel).
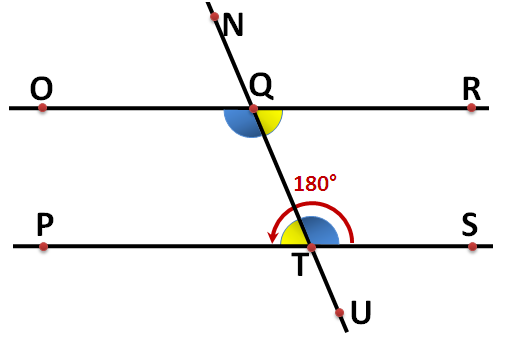
If we extend QR and QT, then we will two parallel line segments and a transversal. In Figure 3, OR and PS are parallel lines a NU is a transversal. From Figure 1 and Figure 2, the yellow angles are corresponding angles, so RQT and PTQ are congruent. We can also see that the blue angle and yellow angle are supplementary (the sum of their measure is 180 degrees).
With the knowledge that the blue angle and the yellow angle are supplementary, we can deduce the following:
- Interior angles on the same side of a transversal of parallel lines (RQT and STQ) are supplementary.
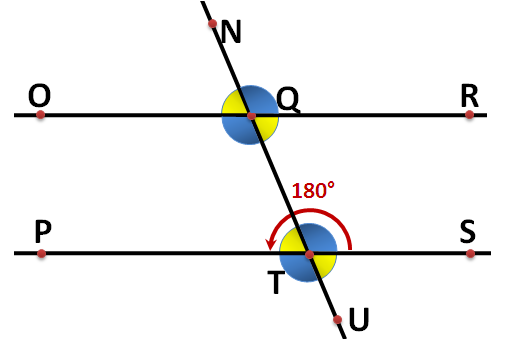
- Angles OQN and OQT are supplementary so NQT must have the same measure as that of the yellow angle.
- Angles RQT and RQN are supplementary so RQN must have have the same measure as that of the blue angle.
- From 2 and 3, it follows that PTU is a blue angle and STU is a yellow angle.
With all the observations and deductions above, we came up with the following diagram. Note that angles symbols with the same color are congruent angles.
Pairs of these angles have special names for distinction purposes. Most of the names are descriptive, so it is easy to determine other pairs. Some pairs of angles and their names are listed below.
1.) TQR and QTS are same side interior angles.
2.) NQR and STU are same side exterior angles.
3.) RQT and PTQ are alternate interior angles.
4.) STU and NQO are alternate exterior angles.
5.) NQO and QTP are corresponding angles.
Parallel lines and its relationship with its interval was mentioned in Euclid’s book The Elements. It is called the Fifth postulate or the Parallel Postulate. The parallel postulate states that
If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.
All the relationships we have deduced above can be derived from this single statement.
I have also written why the angle sum of the interior angles of a triangle is 180 degrees. C