Why is the angle sum of the interior angles of a triangle equal to 180 degrees?

We were taught that the sum of the measures of interior angles of a triangle is 180 degrees. But how come? Is it true no matter what the shape or size of the triangle?

Figure 1 - Triangles with interior angles a, b and c

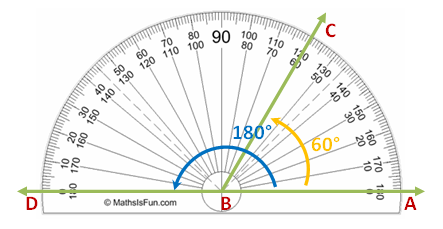
Recall that an angle is the amount of rotation of a ray. In Figure 2, the ray was rotated from A to C, and the amount of rotation is 60 degrees. We can say that the measure of angle ABC is 60 degrees.

Figure 2 - Ray containing A is rotated to to C making a 60-degree angle rotation

The rotation from A to D forms a straight line and measures 180 degrees. Therefore, straight angle ABD measures 180 degrees. It is clear that a 180-degree rotation is a half-circle. Therefore, a complete rotation forming a circle is 360 degrees.

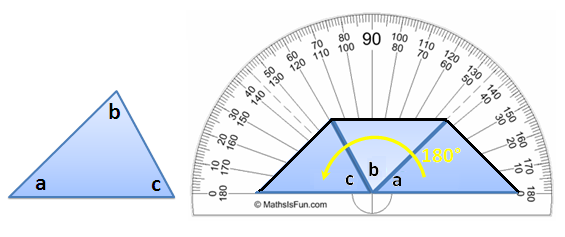
We can verify if our question about the sum of the interior angles of a triangle by drawing a triangle on a paper, cutting the corners, meeting the corners (vertices) in one point such that the sides coincide with no gas and overlaps (see Figure 3). Notice that no matter what the size or shape of a triangle, as long as the previous condition is met, the two of its sides will be collinear as shown in the Figure below.

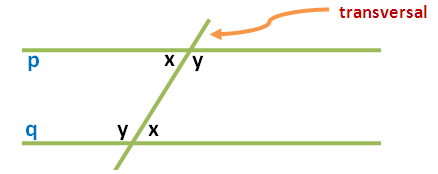
Figure 4 - The corners of a triangle put together

However, this is not the proof. To discuss the proof, we are going to use Euclid’s fifth postulate. Euclid’s fifth postulate tells us that if a parallel line is cut by a transversal, their corresponding angles are congruent. In the diagram below, lines p and q are parallel, and angles shown with the same names are corresponding angles, and hence congruent.

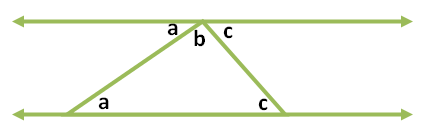
Figure 5 - Parallel lines p and q cut by a transversal.

Using the fifth postulate, we use on base of a triangle and extend it to form a line, and then draw a parallel line to the vertex which is not common to the base as shown in Figure 5. Now, angles a, b and c combined together form a straight angle and is therefore equal to 180 degrees. But a, b and c are also the interior angles of a polygon.