Why is the angle sum of the interior angles of a triangle 180 degrees?
We were taught that the sum of the measures of interior angles of a triangle is 180 degrees. But how come? Is it true no matter what the shape or size of the triangle?
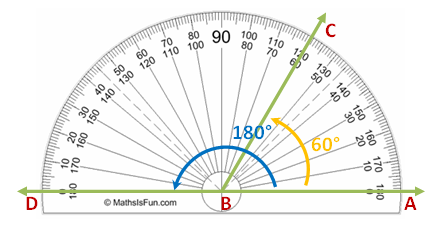
Recall that an angle is the amount of rotation of a ray. In Figure 2, the ray was rotated from A to C, and the amount of rotation is 60 degrees. We can say that the measure of angle ABC is 60 degrees.
The rotation from A to D forms a straight line and measures 180 degrees. Therefore, straight angle ABD measures 180 degrees. It follows that a 180-degree rotation is a half-circle. Therefore, a complete rotation is 360 degrees.
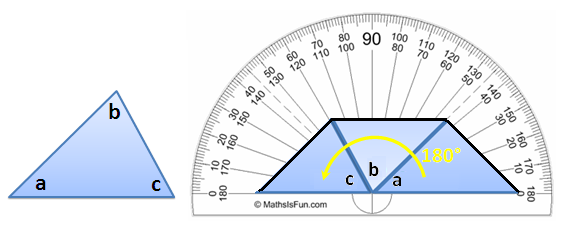
We can verify if our question about the sum of the interior angles of a triangle by drawing a triangle on a paper, cutting the corners, meeting the corners (vertices) at one point such that the sides coincide with no gaps and overlaps (see Figure 3). Notice that no matter what the size or shape of a triangle, as long as the previous conditions are met, the two of its sides will be collinear as shown in the Figure below.
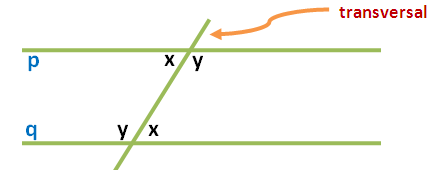
However, this is not the proof. To discuss the proof, we are going to use Euclid’s fifth postulate. Euclid’s fifth postulate tells us that if a parallel line is cut by a transversal, their corresponding angles are congruent. In the diagram below, lines p and q are parallel lines and angles shown with the same letters are corresponding angles, and hence congruent.
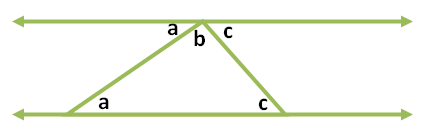
Now how do we connect Parallel Postulate to the angle sum of a triangle. Consider a triangle with interior angles a, b, and c. Using the fifth postulate, we use the side containing angles a and c as base of the triangle and extend it to both sides. Next, we draw a line to the base and passing thorugh the vertex not on the base.
Now, the sum of angles a, b and c is 180 degrees (why?). But a, b and c are also the interior angles of a polygon. Therefore, the sum of the interior angles of a triangle is 180 degrees.
You may also want to read Sum of the Interior Angles of a Polygon.