GeoGebra Tutorial 7 – Sliders and Rotation
This is the seventh tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, please read the GeoGebra Essentials Series.
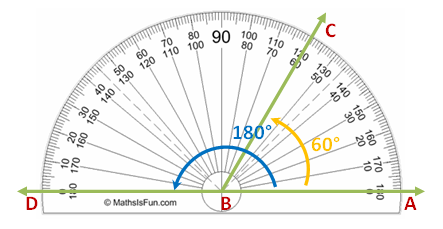
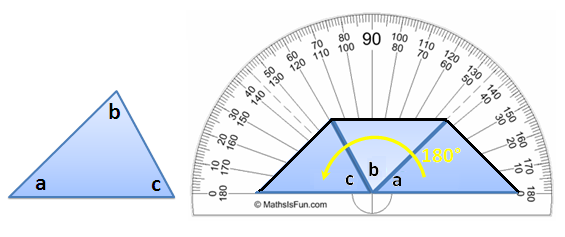
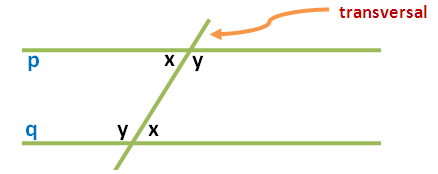
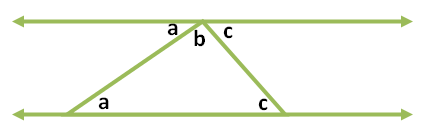
In the Graphs and Sliders posts (click here and here ), we have discussed how to use number sliders. In this tutorial, we use the Angle slider to rotate a triangle in order to show that its angle sum is 180 degrees. This is the same GeoGebra worksheet shown in my Parallel Lines and Transversals post, but we will change some of the labels. Although this tutorial is the seventh of the GeoGebra Tutorial Series.
Construction Overview
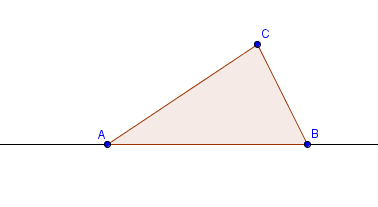
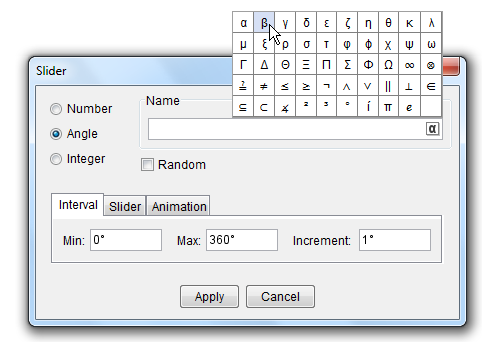
The construction will start by drawing line AB and constructing triangle ABC using the Polygon tool. Afterwards, we reveal the interior angle measures of the triangle and create two angle sliders namely and
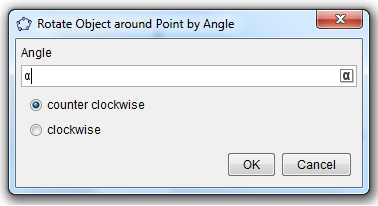
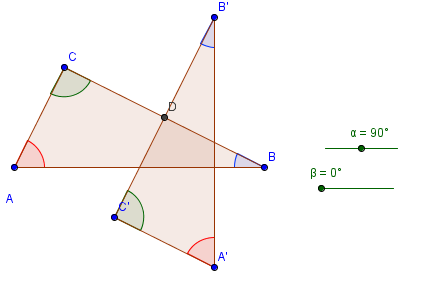
. Next, we rotate the triangle 180 clockwise about the midpoint of BC producing triangle A’B’C’ (see Figure 1-B). We then repeat the process, and rotate triangle A’B’C’ 180 degrees clockwise about the midpoint of A’C’ to produce A’’B’’C’’.
Part I – Constructing Triangle ABC
Part II – Rotating the Triangle
We already have the sliders ready. The next thing that we will do is to rotate the triangle. The idea is to create a rotation point. Our choice would be the midpoint of BC. That is because if we rotate ABC by 180 degrees producing A’B’C’, angle A’C’B’ will be adjacent to angle ABC (see Figure 1-B). This is also the idea when we rotate A’B’C’ producing A’’B’’C’’.
.
Part III – Creating the Third Triangle
The idea of creating the third triangle is basically the same as that of creating the second triangle, so I will just enumerate the steps and left the construction as an exercise.
- Get the midpoint of A’C’. (Refer to Part II Step 1)
- Rotate triangle A’B’C’
degrees clockwise around the midpoint of A’C’. (Refer to Part II – Steps 2 – 3).
- Reveal the labels of the vertices of the third triangle which is A’’B’’C’’. (Refer to Part II – Step 5 and Part I – Step 3).
- Reveal the angle symbols of triangle A’’B’’C’’. (Refer to Part I – Step 11)
- Hide the labels of the angle symbols, and change the colors of the angle symbols of triangle A’’B’’C’’. (Refer to Part I – Step 13-15)
The explanation of the theory behind this construction is in my Parallel Lines and Transversal post.