GeoGebra Tutorial 4 – Graphs and Sliders
This is the fourth tutorial in the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, please read the GeoGebra Essentials Series first.
In this tutorial, we use GeoGebra to investigate the effects of parameters of the equations of functions to the appearance of their graphs. First, we type equations and then use a slider investigate the effects of
.
Graphing Functions
- Open GeoGebra and be sure the the Algebra and Graphics view is selected for the Perspective menu.
- To graph
, type y = 2x in the input field. (The input field is the text box with the label Input located at the bottom of your GeoGebra window.) Press the ENTER key on your keyboard.
- Type the following equations: y = 3x, y = 4x , y = -8x, and press the ENTER key after each equation.
- Type more equations of the form
where
is any real number.
- How does the value of
affect the appearance of the graph of the function
?
Using Sliders
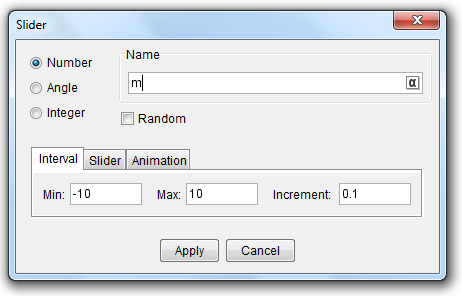
To avoid typing over and over again for varying values , we use the slider tool. A slider is a visual representation of a number. This time, we add the parameter b. This means that we will explore the graph of the function of
, where
and
are real numbers.
Instructions
Notes:
- The ^ symbol is used for exponentiation. Hence, we write
as a*x^2 + c.
- Instead of using
in writing equations of functions, you can also use
for the function
.
Last Update: November 12, 2014 for GeoGebra 5.0.