angle sum of polygons Archives - Math and Multimedia

Angle Sum of Polygons in Tessellated Triangles

November 3, 2013 GB High School Geometry, High School Mathematics, Problem Solving and Proofs

Tessellated triangles are not only beautiful but that they are also interesting. Tessellating them will prove the angle sum of polygons particularly parallelogram, trapezoid, and hexagon. The term angle sum means the sum of the interior angles.

Let us start with the knowledge that the angle sum of a triangle is 180 degrees. Copying a triangle with angle measures x, y, and z, and rotating it 180 degrees will give us the first two figures. The tessellated copies are shown in the next figure.

Using the three figures above, we can prove the following. » Read more

Leave a comment angle sum of parallelograms, angle sum of polygons, angle sum of trapezoid, tessellated triangles

GeoGebra Tutorial 7 – Sliders and Rotation

January 13, 2010 GB High School Geometry, High School Mathematics, Software Tutorials

This is the seventh tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, please read the GeoGebra Essentials Series.

In the Graphs and Sliders posts (click here and here ), we have discussed how to use number sliders. In this tutorial, we use the Angle slider to rotate a triangle in order to show that its angle sum is 180 degrees. This is the same GeoGebra worksheet shown in my Parallel Lines and Transversals post, but we will change some of the labels. Although this tutorial is the seventh of the GeoGebra Tutorial Series.

Figure 1 – Rotated triangles using sliders.

Construction Overview

The construction will start by drawing line AB and constructing triangle ABC using the Polygon tool. Afterwards, we reveal the interior angle measures of the triangle and create two angle sliders namely $\alpha$ and $\beta$ . Next, we rotate the triangle 180 clockwise about the midpoint of BC producing triangle A’B’C’ (see Figure 1-B). We then repeat the process, and rotate triangle A’B’C’ 180 degrees clockwise about the midpoint of A’C’ to produce A’’B’’C’’.

Part I – Constructing Triangle ABC

	1.) Open GeoGebra and select Geometry from the Perspectives menu.
	2.) Click the Line through Two Points tool, and click two distinct locations on the Graphics view to construct line AB.
	3.) If the labels of the points are not displayed, click the Move tool, right click each point and click Show label from the context menu.
	4.) Click the New Point tool and construct a point C not on line AB.
	5.) Display the name of the third point. GeoGebra would automatically name it C, otherwise right click and rename it C.
	6.) Click the Polygon tool and click the points in the following order: point A, point B, point C, and click again on point A to close the polygon. Your drawing should look like Figure 1. Figure 2 – Triangle ABC on line AB.
	7.) Move the vertices of the polygon. What do you observe?
	8.) Now we construct two angle sliders $\alpha$ and $\beta$ . To do this, click the Slider tool, and click on the Graphics view.
	9.) In the Slider dialog box (see Figure 3), choose the Angle radio button, and then leave the name angle as $\alpha$ . In the Interval tab, choose 0° as minimum, 180° as maximum and 1°, and then click the Apply button when finished. Figure 3 – The Slider dialog box
	10.) Using steps 8-9, create another slider with the same specifications shown in Figure 3 and name it $\beta$ . You can find the Greek letters by pressing the $\alpha$ button located at the right of the text box.
	11. ) We reveal the angle measures of the interior angles of the triangle, the change the colors of the angle symbols (green sectors). To do this, click the Angle tool and then click the interior of triangle ABC.
	12.) We now hide the measures of the angles. To do this, right click each angle symbol and uncheck Show label from the context menu.
	13. We set angle colors: angle A red, angle B blue and angle C green. To change the color of the angle symbol of angle A, right click the angle symbol (not point A) and click Object Properties from the context menu to display the Preferences window.
	14. In the Preferences window, click the Color tab and choose the color you want from the color palette then click the Close button.
	15. Change the color of angle B to blue and leave angle C as is. Your drawing should look line Figure 1-A after step 15.

Part II – Rotating the Triangle

We already have the sliders ready. The next thing that we will do is to rotate the triangle. The idea is to create a rotation point. Our choice would be the midpoint of BC. That is because if we rotate ABC by 180 degrees producing A’B’C’, angle A’C’B’ will be adjacent to angle ABC (see Figure 1-B). This is also the idea when we rotate A’B’C’ producing A’’B’’C’’.

	1.) To construct D, the midpoint of BC, click the Midpoint or Center tool, and click side BC (the segment, not the points).
	2.) Note that we want ABC to rotate around D $\alpha$ degrees clockwise. To do this, choose Rotate around a Point by Angle tool, click the interior of the triangle and click point D to reveal the Rotate Object dialog box.
	3.) In the Rotate Object around Point by Angle dialog box, change the measure of the angle to $\alpha$ , choose the clockwise radio button, and then click the OK button. Figure 4 – The Rotate Dialog Box
	4.) Now move slider $\alpha$ . What do you observe?
	5.) Adjust slider $\alpha$ to 90 degrees, and show the labels of the vertices of the rotated triangle. (Refer to Part I – Step 3).
	6.) While the triangle is still rotated 90 degrees, click the Angle tool and click the interior of triangle A’B’C’. Hide the labels of the angles symbols.
	7.) Change the colors of the angle measures. Refer to Part I – Steps 13 through 15. Be sure that angle A and A’ have the same color, B and B’ have the same color, and C and C’ have the same color. Your drawing should look like the drawing in Figure 6. Figure 5 – The Rotated Triangle

Part III – Creating the Third Triangle

The idea of creating the third triangle is basically the same as that of creating the second triangle, so I will just enumerate the steps and left the construction as an exercise.

Get the midpoint of A’C’. (Refer to Part II Step 1)
Rotate triangle A’B’C’ $\beta$ degrees clockwise around the midpoint of A’C’. (Refer to Part II – Steps 2 – 3).
Reveal the labels of the vertices of the third triangle which is A’’B’’C’’. (Refer to Part II – Step 5 and Part I – Step 3).
Reveal the angle symbols of triangle A’’B’’C’’. (Refer to Part I – Step 11)
Hide the labels of the angle symbols, and change the colors of the angle symbols of triangle A’’B’’C’’. (Refer to Part I – Step 13-15)

The explanation of the theory behind this construction is in my Parallel Lines and Transversal post.

19 comments angle sum of a triangle, angle sum of polygons, GeoGebra basics, geogebra slider, GeoGebra Tutorial, geometric transformation, interior angles, interior angles of a triangle, rotation of an object

The Exterior Angle Theorem

December 26, 2009 GB High School Calculus, High School Geometry, High School Mathematics

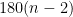In the angle sum of a triangle post, we have discussed that the angle sum of a triangle is $180$ degrees. In the angle sum of a polygon post, we also have discussed that and that the angle sum of a polygon with $n$ sides is $180(n-2)$ . For example, a pentagon has 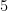$5$ sides, so the sum of its interior angle is $180(5-2) = 180(3) = 540$ degrees.

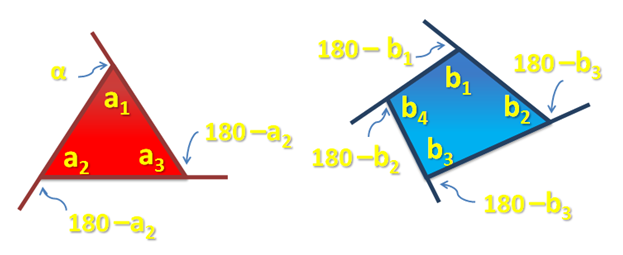
Figure 1 – The interior and exterior angles a triangle and a quadrilateral.

The angle sums that we have discussed in both blogs refer to the sum of the interior angles. What about the exterior angles?

The exterior angle is formed when we extend a side of a polygon. In the triangle above, 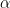$\alpha$ is an exterior angle. The sum of the interior angle and the exterior angle adjacent to it is always $180$ degrees (Why?). Angles whose sum is $180$ degrees are called supplementary angles. If two angles are supplementary, we call them a linear pair. For example, angles 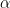$\alpha$ and $a_1$ are supplementary angles and at the same time a linear pair, so $\alpha + a_1 = 180$ degrees. 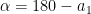Now this means, that $\alpha = 180 - a_1$ .Therefore, if we want to compute the measure of an exterior angle adjacent to an interior angle, we can always subtract the measure of the interior angle from $180$ as shown in Figure 1.

Observe the computation in the two diagrams. If we let 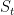$S_t$ be the angle sum of the exterior angles of a triangle, then 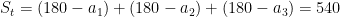$S_t = (180 - a_1) + (180 - a_2) + (180 - a_3) = 540$ . Rearranging the terms, we have 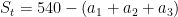$S_t = 540 - (a_1 + a_2 + a_3)$ . But $a_1 + a_2 + a_3$ is the sum of the interior angles of a triangle which is $180$ degrees, so $540 - (a_1 + a_2 + a_3) = 540 - 180 = 360$ degrees.

Now, try calculating for the sum of the exterior angles of the quadrilateral above. What is your answer?

To verify our hunch, we will try to compute for the sum of the exterior angles of a pentagon.

Let 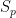$S_p$ be the sum of the exterior angles of the pentagon in Figure 2. Then

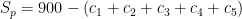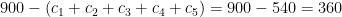$S_p =(180 - c_1)+ (180 - c_2) + (180 - c_3) +(180 - c_4) +(180 - c_5)$ . Simplifying, we have $S_p = 900 - (c_1 + c_2 + c_3 + c_4 + c_5)$ . But according to the angle sum theorem for polygons, $c_1 + c_2 + c_3 + c_4 + c_5 = 540$ . Therefore, $900 - (c_1 + c_2 + c_3 + c_4 + c_5) = 900 - 540 = 360$ degrees.

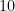We have three polygons – triangle, quadrilateral, pentagon – whose angle sums of exterior angles are always $360$ degrees. Now, is this true for all polygons? Try to compute polygons up to $10$ sides and see if the sum is $360$ degrees.

Delving Deeper

We know that in a polygon, the number of exterior angles is equal to the number of interior angles. Furthermore, we know that the angle sum of an interior angle and the exterior angle adjacent to each is always latex 180 degrees. If we have a polygon with 5 sides, then

interior angle sum + exterior angle sum = 180(5)

In general, this means that in a polygon with n sides

interior angle sum* + exterior angle sum = 180n

But the interior angle sum = 180(n – 2). So, substituting in the preceding equation, we have

180(n – 2) + exterior angle sum = 180n

which means that the exterior angle sum = 180n – 180(n – 2) = 360 degrees. More formal proofs using these arguments are shown below.

Theorem: The sum of the measure of the exterior angles of a polygon with n sides is 360 degrees.

Proof 1:

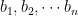Let $a_1, a_2, \cdots a_n$ be measures of the interior angles of a polygon with n sides. Let $b_1, b_2, \cdots b_n$ be measures of the exterior angles of the same polygon where all angle names with the same subscripts are adjacent angles from $a_1$ and $b_1$ all the way up through 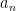$a_n$ and $b_n$ . We know that adjacent interior and exterior angles are supplementary angles, so this implies that their measures add up to 180 degrees. Hence,

(a₁ + b₁) + (a₂ + b₂) + … + (a_n + b_n) = 180 + 180 + … +180 (n of them) = 180n

Regrouping the terms of the preceding equation, we have

(a₁ + a₂ + … + a_n) + (b₁ + b₂ + … + b_n) = 180n

But the sum of the interior angles is a₁ + a₂ + … + a_n = 180(n – 2)

So,

180(n – 2) + (b₁ + b₂ + … + b_n) = 180n

b₁ + b₂ + … + b_n = 180n – 180(n – 2) = 360

Therefore, the sum of the exterior angles of any polygon is equal to 360 degrees.

Proof 2:

Let a₁, a₂, …, a_n be measures of the interior angles of the polygon with n sides. Since each adjacent interior and exterior angle is a linear pair, it follows that the measure of the exterior angles adjacent to them respectively are 180 – a₁, 180 – a₂, …, 180 – a_n.

If we let S, be the sum of the measure of the exterior angles, we have

S = (180 – a₁) + (180 – a₂) + (180 – a₃) + … + (180 – a_n)

= (180 + 180 + 180 + … +180 (n of them)) – a– a₂ – a₃– … – a_n

S = 180n – (a₁+ a₂ + a₃+ … + a_n)

But a₁+ a₂ + a₃+ … + a_nis the sum of the measures of the interior angles of a polygon with n sides which equals

180(n – 2), so, S = 180n – 180(n – 2) = 360, which is want we want to show.

Therefore, the sum of the exterior angles of any polygon is equal to 360 degrees.

Leave a comment angle sum, angle sum of polygons, exterior angle math, exterior angle theorem, exterior angles convex polygon, exterior angles definition, interior angles, linear pair, polygon exterior angle sum theorem, sum of exterior angles of a polygon, sum of interior angles, triangle angle sum

1 2 »