Tag: angle sum of parallelograms

Angle Sum of Polygons in Tessellated Triangles

High School Geometry, High School Mathematics, Problem Solving and Proofs

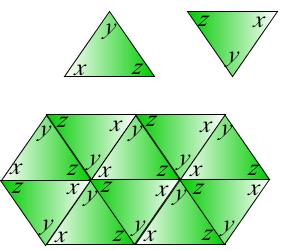
Tessellated triangles are not only beautiful but that they are also interesting. Tessellating them will prove the angle sum of polygons particularly parallelogram, trapezoid, and hexagon. The term angle sum means the sum of the interior angles.

Let us start with the knowledge that the angle sum of a triangle is 180 degrees. Copying a triangle with angle measures x, y, and z, and rotating it 180 degrees will give us the first two figures. The tessellated copies are shown in the next figure.

tessellated triangle

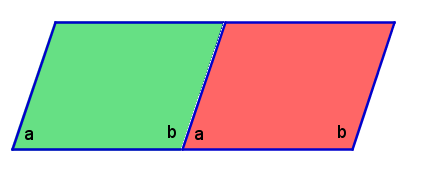
Using the three figures above, we can prove the following.  » Read more

Leave a comment , , ,

Discovering properties of angles of parallelograms

High School Geometry, High School Mathematics

Consider the parallelogram below. We mark the bottom-left angle with a and the bottom-right angle with b to denote their measures as shown in Figure 1.

Figure 1

We create another parallelogram with same size and the shame shape, but of different color. We place the two parallelograms side by side as shown in Figure 2. The angles a and b is a linear pair; therefore, (1) a  + b = 180˚

Figure 2

We create two more parallelograms and place them as shown in Figure 3 to form a bigger parallelogram. Angle a in the red parallelogram and the adjacent angle in the blue parallelogram is also a linear pair; therefore, the upper-left angle in the blue parallelogram also equals b (see Figure 4).  In effect, the the upper-right angle in the yellow parallelogram also equals the measure of angle a. » Read more

One comment , ,