Angle Sum of Polygons in Tessellated Triangles

Tessellated triangles are not only beautiful but that they are also interesting. Tessellating them will prove the angle sum of polygons particularly parallelogram, trapezoid, and hexagon. The term angle sum means the sum of the interior angles.

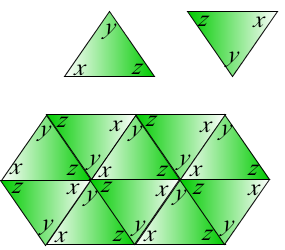
Let us start with the knowledge that the angle sum of a triangle is 180 degrees. Copying a triangle with angle measures x, y, and z, and rotating it 180 degrees will give us the first two figures. The tessellated copies are shown in the next figure.

Using the three figures above, we can prove the following. 

1.) The angle sum of parallelograms is 360 degrees.

Looking at the next figure, we add all the angle measures. Notice that in adding all the angle measures, we are actually adding the angle sums of two triangles.

(x + y + z) + (x + y + z) = 180  + 180 = 360 degrees.

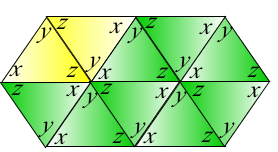
2.) The angle sum of trapezoids is 360 degrees.

In this figure, we add all the angles in the figure and subtract the angles whose representation are colored red (Why?).

That is

(x + y + z) + (x + y + z) + (x + y + z) – (x + y + z) = 540 – 180 = 360

degrees.

Of course, we can just add all the angle measures in the corners of the trapezoid which is equal to

(x + y +z) + (x + y + z) = 360 degrees.

 

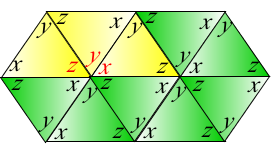
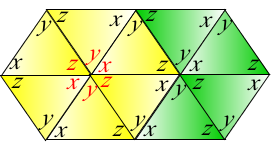
3.) The angle sum of hexagons is 720 degrees.

Just like in 2, we can add up all the numbers in the corner which is equal to 6 (x + y + z) = 6(180) = 720. We can also add up all the angle sum of the 6 triangles and subtract the angle measures represented by red letters. That is

6(x + y + z) – 2(x + y + z) = 4(x + y + z) = 4(180) = 720 degrees.

From above, we can relate the number of vertices of a polygon and its angle sum. Observe and see if you can find a pattern.

triangle (3 vertices): 180 degrees

parallelogram and trapezoid (4 vertices): 360 degrees

hexagon (6 vertices): 720 degrees

Do you think you can find the angle sum of any polygon (don’t click the link if you want to solve it) using the angle measures above?