Discovering properties of angles of parallelograms
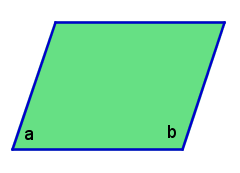
Consider the parallelogram below. We mark the bottom-left angle with a and the bottom-right angle with b to denote their measures as shown in Figure 1.
Figure 1
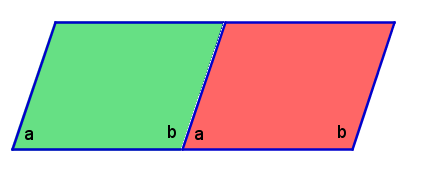
We create another parallelogram with same size and the shame shape, but of different color. We place the two parallelograms side by side as shown in Figure 2. The angles a and b is a linear pair; therefore, (1) a + b = 180˚
Figure 2
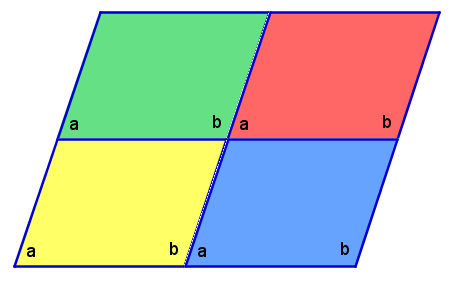
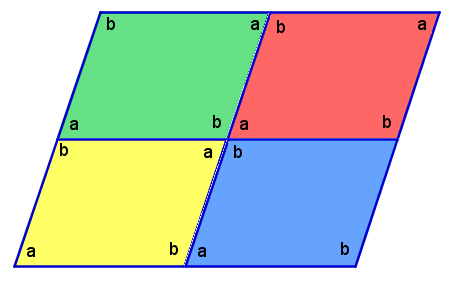
We create two more parallelograms and place them as shown in Figure 3 to form a bigger parallelogram. Angle a in the red parallelogram and the adjacent angle in the blue parallelogram is also a linear pair; therefore, the upper-left angle in the blue parallelogram also equals b (see Figure 4). In effect, the the upper-right angle in the yellow parallelogram also equals the measure of angle a.
Figure 3
In Figure 4, the parallelograms meet at a point with no gaps and overlaps which means that all the angle measures add up to 360 degrees. This is supported algebraically by (1):
(a + b) + (a + b) = 2(a+b) = 360˚.
It is clear that given the measures of the angles in Figure 3, it is possible to give the measures the other angles as shown in Figure 4. We name the angles at the opposite side of the intersecting lines or segments vertical angles.
Figure 4
From Figure 4, we can conclude that
- The consecutive angles of a parallelogram add up to 180 degrees;
- Vertical angles are congruent;
- The opposite angles of a parallelogram are congruent; and
- The angle sum of a parallelogram is 360 degrees.