The Exterior Angle Theorem
In the angle sum of a triangle post, we have discussed that the angle sum of a triangle is degrees. In the angle sum of a polygon post, we also have discussed that and that the angle sum of a polygon with
sides is
. For example, a pentagon has
sides, so the sum of its interior angle is
degrees.
The angle sums that we have discussed in both blogs refer to the sum of the interior angles. What about the exterior angles?
The exterior angle is formed when we extend a side of a polygon. In the triangle above, is an exterior angle. The sum of the interior angle and the exterior angle adjacent to it is always
degrees (Why?). Angles whose sum is
degrees are called supplementary angles. If two angles are supplementary, we call them a linear pair. For example, angles
and
are supplementary angles and at the same time a linear pair, so
degrees. Now this means, that
. Therefore, if we want to compute the measure of an exterior angle adjacent to an interior angle, we can always subtract the measure of the interior angle from
as shown in Figure 1.
Observe the computation in the two diagrams. If we let be the angle sum of the exterior angles of a triangle, then
. Rearranging the terms, we have
. But
is the sum of the interior angles of a triangle which is
degrees, so
degrees.
Now, try calculating for the sum of the exterior angles of the quadrilateral above. What is your answer?
To verify our hunch, we will try to compute for the sum of the exterior angles of a pentagon.
Let be the sum of the exterior angles of the pentagon in Figure 2. Then
. Simplifying, we have
. But according to the angle sum theorem for polygons,
. Therefore,
degrees.
We have three polygons – triangle, quadrilateral, pentagon – whose angle sums of exterior angles are always degrees. Now, is this true for all polygons? Try to compute polygons up to
sides and see if the sum is
degrees.
Delving Deeper
We know that in a polygon, the number of exterior angles is equal to the number of interior angles. Furthermore, we know that the angle sum of an interior angle and the exterior angle adjacent to each is always latex 180 degrees. If we have a polygon with 5 sides, then
interior angle sum + exterior angle sum = 180(5)
In general, this means that in a polygon with n sides
interior angle sum* + exterior angle sum = 180n
But the interior angle sum = 180(n – 2). So, substituting in the preceding equation, we have
180(n – 2) + exterior angle sum = 180n
which means that the exterior angle sum = 180n – 180(n – 2) = 360 degrees. More formal proofs using these arguments are shown below.
Theorem: The sum of the measure of the exterior angles of a polygon with n sides is 360 degrees.
Proof 1:
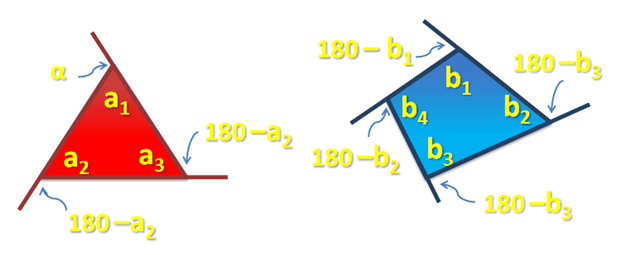
Let be measures of the interior angles of a polygon with n sides. Let
be measures of the exterior angles of the same polygon where all angle names with the same subscripts are adjacent angles from
and
all the way up through
and
. We know that adjacent interior and exterior angles are supplementary angles, so this implies that their measures add up to 180 degrees. Hence,
(a1 + b1) + (a2 + b2) + … + (an + bn) = 180 + 180 + … +180 (n of them) = 180n
Regrouping the terms of the preceding equation, we have
(a1 + a2 + … + an) + (b1 + b2 + … + bn) = 180n
But the sum of the interior angles is a1 + a2 + … + an = 180(n – 2)
So,
180(n – 2) + (b1 + b2 + … + bn) = 180n
b1 + b2 + … + bn = 180n – 180(n – 2) = 360
Therefore, the sum of the exterior angles of any polygon is equal to 360 degrees.
Proof 2:
Let a1, a2, …, an be measures of the interior angles of the polygon with n sides. Since each adjacent interior and exterior angle is a linear pair, it follows that the measure of the exterior angles adjacent to them respectively are 180 – a1, 180 – a2, …, 180 – an.
If we let S, be the sum of the measure of the exterior angles, we have
S = (180 – a1) + (180 – a2) + (180 – a3) + … + (180 – an)
= (180 + 180 + 180 + … +180 (n of them)) – a – a2 – a3– … – an
S = 180n – (a1 + a2 + a3 + … + an)
But a1 + a2 + a3 + … + an is the sum of the measures of the interior angles of a polygon with n sides which equals
180(n – 2), so, S = 180n – 180(n – 2) = 360, which is want we want to show.
Therefore, the sum of the exterior angles of any polygon is equal to 360 degrees.