This is the seventh tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, please read the GeoGebra Essentials Series.
In the Graphs and Sliders posts (click here and here ), we have discussed how to use number sliders. In this tutorial, we use the Angle slider to rotate a triangle in order to show that its angle sum is 180 degrees. This is the same GeoGebra worksheet shown in my Parallel Lines and Transversals post, but we will change some of the labels. Although this tutorial is the seventh of the GeoGebra Tutorial Series.

Figure 1 – Rotated triangles using sliders.
Construction Overview
The construction will start by drawing line AB and constructing triangle ABC using the Polygon tool. Afterwards, we reveal the interior angle measures of the triangle and create two angle sliders namely 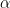 and
and 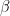 . Next, we rotate the triangle 180 clockwise about the midpoint of BC producing triangle A’B’C’ (see Figure 1-B). We then repeat the process, and rotate triangle A’B’C’ 180 degrees clockwise about the midpoint of A’C’ to produce A’’B’’C’’.
. Next, we rotate the triangle 180 clockwise about the midpoint of BC producing triangle A’B’C’ (see Figure 1-B). We then repeat the process, and rotate triangle A’B’C’ 180 degrees clockwise about the midpoint of A’C’ to produce A’’B’’C’’.
Part I – Constructing Triangle ABC
|
1.) Open GeoGebra and select Geometry from the Perspectives menu. |
 |
2.) Click the Line through Two Points tool, and click two distinct locations on the Graphics view to construct line AB. |
 |
3.) If the labels of the points are not displayed, click the Move tool, right click each point and click Show label from the context menu. |
 |
4.) Click the New Point tool and construct a point C not on line AB. |
|
5.) Display the name of the third point. GeoGebra would automatically name it C, otherwise right click and rename it C. |
 |
6.) Click the Polygon tool and click the points in the following order: point A, point B, point C, and click again on point A to close the polygon. Your drawing should look like Figure 1.
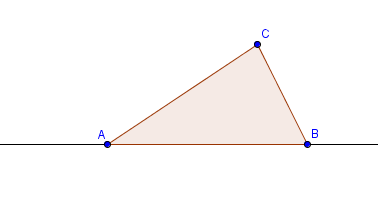 Figure 2 – Triangle ABC on line AB. |
 |
7.) Move the vertices of the polygon. What do you observe? |
 |
8.) Now we construct two angle sliders 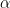 and and 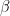 . To do this, click the Slider tool, and click on the Graphics view. . To do this, click the Slider tool, and click on the Graphics view. |
|
9.) In the Slider dialog box (see Figure 3), choose the Angle radio button, and then leave the name angle as 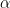 . In the Interval tab, choose 0° as minimum, 180° as maximum and 1°, and then click the Apply button when finished. . In the Interval tab, choose 0° as minimum, 180° as maximum and 1°, and then click the Apply button when finished.
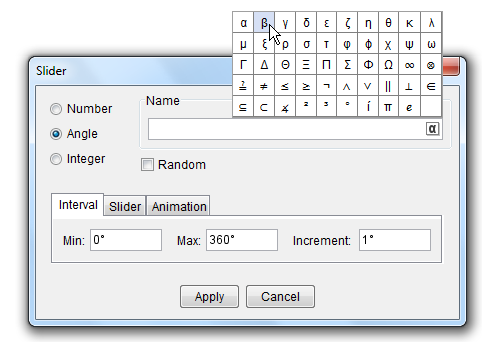 Figure 3 – The Slider dialog box |
 |
10.) Using steps 8-9, create another slider with the same specifications shown in Figure 3 and name it 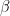 . You can find the Greek letters by pressing the . You can find the Greek letters by pressing the 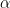 button located at the right of the text box. button located at the right of the text box. |
 |
11. ) We reveal the angle measures of the interior angles of the triangle, the change the colors of the angle symbols (green sectors). To do this, click the Angle tool and then click the interior of triangle ABC. |
|
12.) We now hide the measures of the angles. To do this, right click each angle symbol and uncheck Show label from the context menu. |
|
13. We set angle colors: angle A red, angle B blue and angle C green. To change the color of the angle symbol of angle A, right click the angle symbol (not point A) and click Object Properties from the context menu to display the Preferences window. |
|
14. In the Preferences window, click the Color tab and choose the color you want from the color palette then click the Close button. |
|
15. Change the color of angle B to blue and leave angle C as is. Your drawing should look line Figure 1-A after step 15. |
Part II – Rotating the Triangle
We already have the sliders ready. The next thing that we will do is to rotate the triangle. The idea is to create a rotation point. Our choice would be the midpoint of BC. That is because if we rotate ABC by 180 degrees producing A’B’C’, angle A’C’B’ will be adjacent to angle ABC (see Figure 1-B). This is also the idea when we rotate A’B’C’ producing A’’B’’C’’.
.
 |
1.) To construct D, the midpoint of BC, click the Midpoint or Center tool, and click side BC (the segment, not the points). |
 |
2.) Note that we want ABC to rotate around D 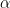 degrees clockwise. To do this, choose Rotate around a Point by Angle tool, click the interior of the triangle and click point D to reveal the Rotate Object dialog box. degrees clockwise. To do this, choose Rotate around a Point by Angle tool, click the interior of the triangle and click point D to reveal the Rotate Object dialog box. |
|
3.) In the Rotate Object around Point by Angle dialog box, change the measure of the angle to 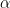 , choose the clockwise radio button, and then click the OK button. , choose the clockwise radio button, and then click the OK button.
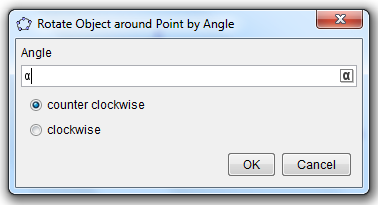 Figure 4 – The Rotate Dialog Box |
 |
4.) Now move slider 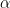 . What do you observe? . What do you observe? |
 |
5.) Adjust slider 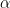 to 90 degrees, and show the labels of the vertices of the rotated triangle. (Refer to Part I – Step 3). to 90 degrees, and show the labels of the vertices of the rotated triangle. (Refer to Part I – Step 3). |
 |
6.) While the triangle is still rotated 90 degrees, click the Angle tool and click the interior of triangle A’B’C’. Hide the labels of the angles symbols. |
|
7.) Change the colors of the angle measures. Refer to Part I – Steps 13 through 15. Be sure that angle A and A’ have the same color, B and B’ have the same color, and C and C’ have the same color. Your drawing should look like the drawing in Figure 6.
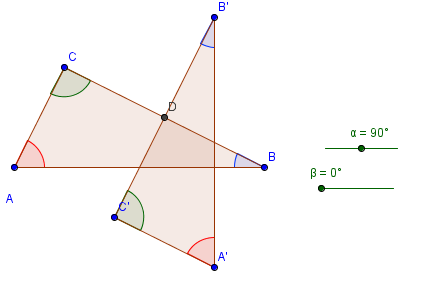 Figure 5 – The Rotated Triangle |
Part III – Creating the Third Triangle
The idea of creating the third triangle is basically the same as that of creating the second triangle, so I will just enumerate the steps and left the construction as an exercise.
- Get the midpoint of A’C’. (Refer to Part II Step 1)
- Rotate triangle A’B’C’
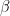 degrees clockwise around the midpoint of A’C’. (Refer to Part II – Steps 2 – 3).
degrees clockwise around the midpoint of A’C’. (Refer to Part II – Steps 2 – 3).
- Reveal the labels of the vertices of the third triangle which is A’’B’’C’’. (Refer to Part II – Step 5 and Part I – Step 3).
- Reveal the angle symbols of triangle A’’B’’C’’. (Refer to Part I – Step 11)
- Hide the labels of the angle symbols, and change the colors of the angle symbols of triangle A’’B’’C’’. (Refer to Part I – Step 13-15)
The explanation of the theory behind this construction is in my Parallel Lines and Transversal post.
and
. Next, we rotate the triangle 180 clockwise about the midpoint of BC producing triangle A’B’C’ (see Figure 1-B). We then repeat the process, and rotate triangle A’B’C’ 180 degrees clockwise about the midpoint of A’C’ to produce A’’B’’C’’.
degrees clockwise around the midpoint of A’C’. (Refer to Part II – Steps 2 – 3).




