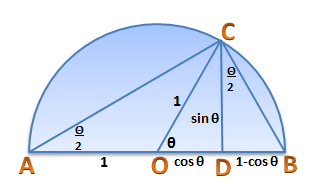
inscribed angle theorem Archives - Math and Multimedia

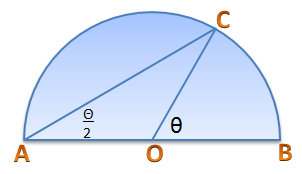
How to Find the Center of a Circle and The Mathematics Behind

July 20, 2013 GB High School Geometry, High School Mathematics

Finding the center of a circle can be quite tricky in some cases, but has a practical and important applications. For instance, an ancient broken plate is unearthed and the archaeologist wants to find the length of its diameter, he can just find its center. Once the center is found, he can also find the length of the radius and hence can find the length of the diameter.

In this post, we learn how to find the center of the circle in different ways. » Read more

2 comments find the center of a circle mathematically, find the center of a circle using three points, finding the center of a circle, how to find the center of a circle, inscribed angle theorem, perpendicular bisector

A Proof that the Vertex Angle Sum of a Pentagram is 180 degrees

June 23, 2012 GB High School Geometry, High School Mathematics

The pentagram is a five-pointed star. It was used by the ancient Greeks as a symbol of faith. In this post, we exhibit the mathematics of pentagrams — we show that the sum of the angle measures of its vertices equals 180°.

$pentagram math$

For regular pentagrams, the proof is simple. By the inscribed angle theorem, the measure of an inscribed angle is half the measure of a central angle that intercepts the same arc. The central angles of a regular pentagram as shown above intercept the entire circle. Therefore, its angle measures add up to 360°.

The vertex angles, on the other hand, are inscribed angles as shown in the second image above. Notice that if we add them up, they also intercept the entire circle (Can you see why?). In effect, their angle sum is half of 360°, which equals 180°. » Read more

4 comments angle sum of a 5-pointed start, equilateral triangle, exterior angle theorem, inscribed angle theorem, vertex angle sum of a pentagram

The Proof of the Tangent Half-Angle Formula

May 3, 2012 GB High School Mathematics, High School Trigonometry, Problem Solving and Proofs

In this post, we prove the following trigonometric identity:

$\displaystyle \tan \frac{\theta}{2} = \frac{\sin\theta}{1 + \cos \theta} = \frac{1 - \cos \theta}{\sin \theta}$ .

Proof

Consider a semi-circle with “center” $O$ and diameter $AB$ and radius equal to 1 unit as shown below. If we let $\angle BOC =\theta$ , then by the Inscribed Angle Theorem, $\angle CAB = \frac{\theta}{2}$ .

Draw $CD$ perpendicular to $OB$ as shown in the second figure. We can compute for the sine and cosine of $\theta$ which equal to the lengths of $CD$ and $OD$ , respectively. In effect, $BD = 1 - \cos \theta$ and $AD = 1 + \cos \theta$ . » Read more

2 comments half angle formula, half angle formula identity, half angle formula proof, inscribed angle theorem, proof without words, trigonometric identities, trigonometric identity

1 2 »