A Proof that the Vertex Angle Sum of a Pentagram is 180 degrees
The pentagram is a five-pointed star. It was used by the ancient Greeks as a symbol of faith. In this post, we exhibit the mathematics of pentagrams — we show that the sum of the angle measures of its vertices equals 180°.
For regular pentagrams, the proof is simple. By the inscribed angle theorem, the measure of an inscribed angle is half the measure of a central angle that intercepts the same arc. The central angles of a regular pentagram as shown above intercept the entire circle. Therefore, its angle measures add up to 360°.
The vertex angles, on the other hand, are inscribed angles as shown in the second image above. Notice that if we add them up, they also intercept the entire circle (Can you see why?). In effect, their angle sum is half of 360°, which equals 180°.
For non-regular pentagrams , we use the exterior angle theorem which states that the measure of the exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
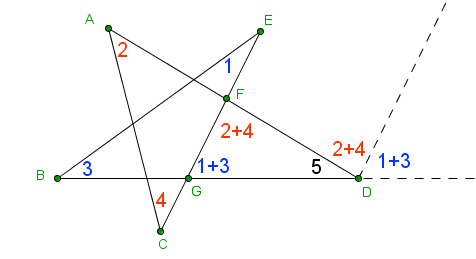
In the second figure, by exterior angle theorem, m ∠FGD = m ∠ 1 + m ∠ 3, since angles ∠1 and ∠3 are its remote angles. Similarly, m ∠ GFD = m ∠ 2 + m ∠ 4 since it is an exterior angle with remote angles 2 and 4.
Now, the sum of the interior angles of triangle FGD = m ∠ 1 + m ∠ 3 + m ∠ 2 + m ∠ 4 + m ∠ 5 = 180°. But these are the angles of the pentagram. Therefore, the angle sum of the vertices of a pentagram is equal to 180°.
The extended line segment and the line segment parallel to CE denoted by the dashed lines also show that the angles labeled 1 + 3, 2 + 4, and 5 form a straight angle. With respect to the parallel line segments, the two angles labeled 2 + 4 are alternate interior angles, and the two angles labeled 1 + 3 are same side exterior angles.