How to Find the Center of a Circle and The Mathematics Behind
Finding the center of a circle can be quite tricky in some cases, but has a practical and important applications. For instance, an ancient broken plate is unearthed and the archaeologist wants to find the length of its diameter, he can just find its center. Once the center is found, he can also find the length of the radius and hence can find the length of the diameter.

In this post, we learn how to find the center of the circle in different ways.
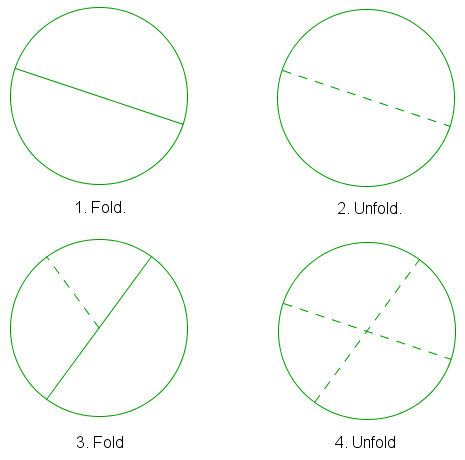
Method 1: By Folding
If the circle is made of paper, finding the center can be easy. Just fold the circle at the center to form a semicircle. Since the fold is the longest chord (why?), then it is a diameter and therefore passes through the center of the circle.
So, making another fold different from the first one will intersect the first fold. The intersection is the center of the circle.
Method 2: Getting the Perpendicular Bisector
Draw a chord and get its perpendicular bisector. Draw another chord different from the first one, and then draw its perpendicular bisector.
The intersection of the two perpendicular bisectors is the center of the circle.
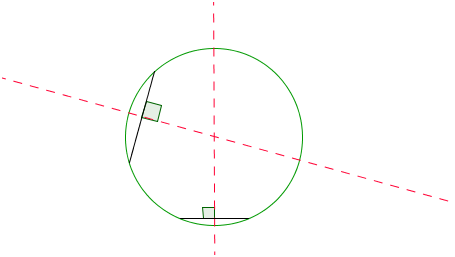
Method 3: Using a Right Triangle
Draw point on the circle and draw a right angle with it as vertex. Extend the sides of the angle such that they intersect the circumference of the circle. The intersections are end points of a diameter of a circle.
Repeat this process using another point as vertex on the circle to draw another diameter. Again, the intersection of the two diameters is the center of the circle.
The Mathematical Ideas Behind
Method 1
The diameter of a circle which is its line of symmetry divides it into two congruent parts. Therefore, the fold made in Method 1 is a diameter of the circle.
Method 2
The second method can be used to find the center of the circle because the perpendicular bisector of a circle passes through the center of the circle. For now, accept this by faith; I will discuss the proof in the next post.
Method 3
The inscribed angle theorem states that an inscribed angle is half the measure of its intercepted arc. So, angle BAC intercepts 180° or half the circle. Therefore, BC is the diameter. Again the intersection of the two diameters is the center of the circle, so this method can be used to find its center.
Image Credit: Letters from the Armory