The Proof of the Tangent Half-Angle Formula
In this post, we prove the following trigonometric identity:
.
Proof
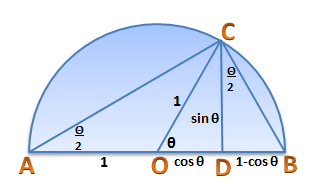
Consider a semi-circle with “center” and diameter
and radius equal to 1 unit as shown below. If we let
, then by the Inscribed Angle Theorem,
.
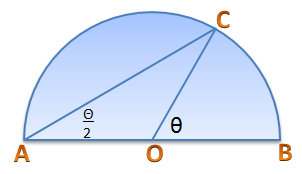
Draw perpendicular to
as shown in the second figure. We can compute for the sine and cosine of
which equal to the lengths of
and
, respectively. In effect,
and
.
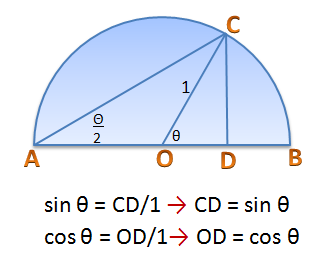 Draw
Draw . Notice that
and
are similar triangles, so their corresponding angles are congruent. So,
.
Now, we compute for the tangent of .
In triangle ,
.
In triangle ,
.
Therefore,
.
And we are done.
***
The last figure is the proof without words of R. J. Walker.