GeoGebra Tutorial 14 – Sliders and Circle-Area Approximation

This is the 14th tutorial in the GeoGebra Tutorial Series. If this is your first time to use GeoGebra, I suggest that you read the GeoGebra Essentials series first.

In this tutorial, we use GeoGebra to approximate the area of a circle.  This strategy of approximating the area of a circle was used by the Greek mathematician Archimedes.

Since this tutorial is long, we split it into two parts. In Part I, we inscribe a regular polygon in a circle, increase its number of sides, and investigate the relationship between the areas. In Part II we will circumscribe the circle with a regular polygon increase its number of sides to approximate the circle’s area.  Before following the tutorial step-by-step, click here to view the final output.

Part I – Creating an Inscribed Polygon

Step-by-Step Instructions

	1. Open GeoGebra click on Algebra & Graphics in the Perspectives menu.
	2. In this tutorial, we want all new objects to be labeled. To do this, click the Options menu, click Labeling, then click on All New Objects.
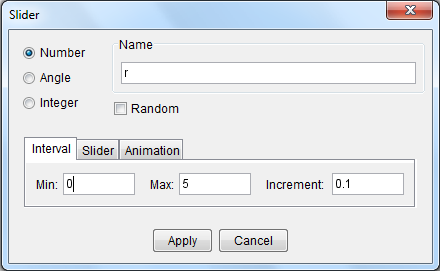
	3. Next, we create  slider r that will determine the radius of the circle that we are about to create.  Select the Slider tool, then click anywhere on the Graphics view to display the Slider dialog box.
	4. In the Slider dialog box, type r in the Name box, type 0.1 in the min box, and leave the max value as 5 and increment as 0.1, then click the Apply button.
	5. Create another slider name it n, set the minimum to 3, maximum to 30 and increment to 1. Slider n will determine the number of sides of the inscribed polygon.
	6. Next, we create point A on the origin. To do this, select the Intersect Two Objects Tool, click the x-axis and then click the y-axis.
	7. To construct a circle with center A and radius r, type circle[A,r] . Move slider r and observe what happens.
	8. To construct point B which is the intersection of the circle and the x-axis, type B = (r,0) in the input box and press the ENTER/RETURN key on the keyboard.
	9. Now, we compute for the central angle of the inscribed polygon. To do this, we divide 360 by n. For example, if we want to have an equilateral triangle, we must divide 360 by 3, which will be the central angle. To do this, type a = (360/n)° then press the ENTER key. The degree sign, tells GeoGebra that a is an angle measure. You can display the ° sign can be written by clicking the button at the right of the input box.
	10.  To create angle BAB’, click the Angle with Given Size tool, click on point B and then click on point A. This will display the Angle with Given Size dialog box.
	11.  In the Angle dialog box, type a in the Angle text box,  choose the counterclockwise option, and then click the OK button. If you set r to 3, your drawing should look like the one shown in Figure 2. 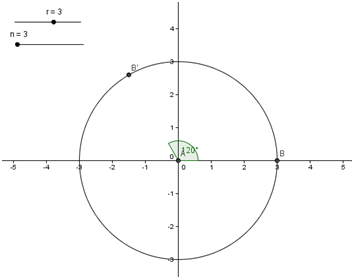Figure 2 – Central angle BAB’.
	12.  To hide the angle measure (green sector), right click it then click Show Object.
	13.  To construct the inscribed polygon, select the Regular Polygon tool, click B and then click B’. This will display the Regular Polygon dialog box.
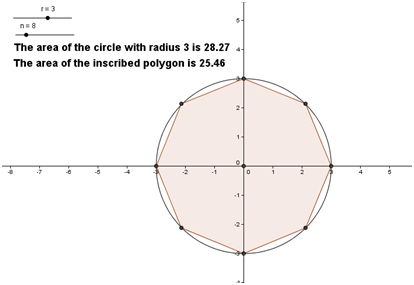
	14.  In the Regular Polygon dialog box, type n and then click the OK button. Now, drag slider n and see what happens. If you set n to 30 and a to 3, the figure should look like Figure 3. 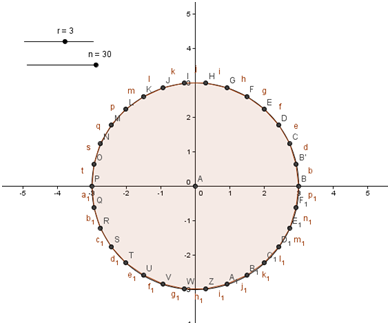Figure 3 – A circle with an inscribed 30-sided polygon.
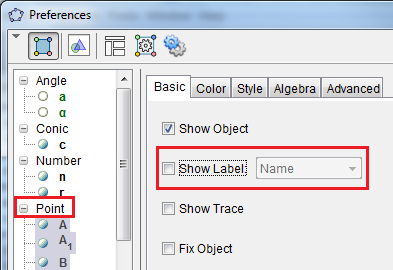
	15.  The problem now is to hide the labels of all the points and the segments. With n set to 30, right click the polygon, then click Object Properties from the context menu to display the Preferences dialog box.
	16.  In the Preferences dialog box, select the Basic tab, click Point (be sure that the Point text is highlighted) in the Objects list, and uncheck the Show Label check box. This will hide the labels of all the points. Now, click Segment text in the Objects check box and uncheck the Show Label check box to hide the labels of all the sides of the polygons, then click the Close button. Figure 4 – The GeoGebra Preferences dialog box.

Exercise:

1. Move the slider and observe what happens.
2. Using the text tool, display the area of the circle and the area of the inscribed triangle.Your drawing should look like Figure 5.