Making Sense of Exponential Growth
Money on Chess Squares
A chessboard has 64 squares. If we are going to place 1 cent in the first square, 2 cents in the second square, 4 cents in the third square, and so on, how much money do we need to fill all the 64 squares?
From the pattern above, it is clear that the amount of money placed in each square is twice than that of the amount placed in the preceding square. If we are going to number the squares from 1 through 64, then the amount of money needed to be placed in each square is shown in the table below.
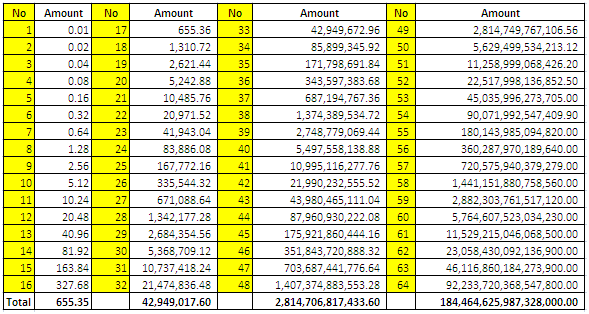
As we can see from the table, the amount of money in the 64th square is 184,464,625,987,328,000.00. If we have indeed placed the money, the total money on our chess board is

Surprised?
How large is our money?
In US Dollars
 The current world population, as of this writing, according to the US Census Bureau is approximately 6.8 billion. Dividing the total amount of money on our chessboard by the total world population, we can see that each person will receive $27, 127, 564.81. That makes everyone a millionaire.
The current world population, as of this writing, according to the US Census Bureau is approximately 6.8 billion. Dividing the total amount of money on our chessboard by the total world population, we can see that each person will receive $27, 127, 564.81. That makes everyone a millionaire.
According to Wikipedia, the federal budge for 2010 of the US is amounting to 3.55 trillion dollars. If we are going to use all the money on our chessboard, the US will have enough budget for 51,962 years.
In Philippine Pesos
Assuming that the money is in Philippine pesos. In 2009, the government budget of the Philippines is approximately 1,300,000,000,000.00 (1.3 trillion pesos) for the entire year. That means that if we actually have that amount of money, and suppose that we maintain the yearly budget to 1.3 trillion, we will have more than enough budget for the next 141,898 years!
How about rice grains?

If instead of 1 cent, we place 1 grain of rice in the first square, 2 grains in the second square, 4 grains in the third square, and so on, the total number of grains placed on
the entire chessboard is 264 − 1 = 18,446,744,073,709,551,615 grains of rice (see Geometric Series) or approximately weighs 461,168,602,000 metric tons (461,168,602,000,000 kilograms), the heap of which is larger than Mount Everest (Source: Wikipedia).
Now, the average life span of a Filipino is 70 years (25, 550 days). If each person eats half kilo a day (that’s an overestimation, I think it’s only a third of a kilogram), then the average rice consumption of a Filipino in 70 years is 12, 775 kilograms.

If we are going to divide 461,168,602,000,000 kilograms of rice by the average lifetime consumption of a Filipino, the answer is 36,099,303,483. That means that the total amount of rice can feed more than 36 billion people in their lifetime. As we have mentioned, the population of the world as of this writing is only 6.8 billion. If all the people in the world have the same average life span and the same average rice consumption as Filipinos, the rice on our chessboard will feed the world for approximately 370 years!
The examples above show the unimaginable rapid growth in numbers. Both examples shows the numbers 2n where n are integers. This fast growth is known as exponential growth.
Note: I have noticed in the 51st number that the decimal place became 0.20 instead of 0.24. I think this is a MS Excel error. It’s probably having a hard time handing large numbers. The error though is not that significant in our analysis and computations.
Photo: Knight Glass Chess Piece by Steven Depolo Making Money by Photo8.com, Mount Everest by Wikipedia, A bowl of Rice by IRRI
Related Articles
- Geometric Sequences and Series
- Compound Interest and the Irrational Number e
- Large Numbers and One Million