A Gentle Introduction to Probability

Sisters’ Dilemma: Who’s going to grandma?

Issa and Ishi go to their grandmother every weekend. Next weekend, however, their mother will be leaving for an important errand, so only one of them will be allowed to go. Both sisters wanted to go, so to decide, they agreed to a toss coin. If the result is head, then Issa will go, otherwise Ishi will.

Tossing a coin would only result to two possible outcomes: a head or a tail. Assuming that the coin is “fair” (we will talk about what we mean by fair later post in the series), the chance of Issa winning the toss coin is 1 out of 2, or 50 percent. From the context, intuition tells us that the chance of Issa winning is the ratio of the number of outcomes favorable to her (that is getting a head) to the total number of possible outcomes (head and tail). Needless to say, Ishi has the same chance of winning.

In mathematical language, we say that the probability of Issa going to her grandmother this coming weekend is 1 out of 2, ½ or 50%. Getting a head in  a toss coin is called an event. We can see that the probability of an event to happen (say, probability of getting a tail in a toss coin or getting a 1 in rolling a die) is the number of favorable outcomes over the number of all possible outcomes.

Ishi, however, thought of a different game.  She said that toss coin is so boring, so why not roll two cubical dice.

Here’s the deal:

If the sum of number of dots is an odd number, then she goes; if the sum is even, Issa goes.

Having thought about it for quite a while, Issa seems uneasy. There are 11 possible sums: 2,  3,  4, 5, 6, 7, 8, 9, 10, 11 and 12. It seems that tossing a die will favor the even sums since there are 6 of them compared to only 5 odd sums. Also, there is no way to divide the sums equally.

Ishi, on the other hand insists that the deal is fair.

Which of the sisters is correct? Try to analyze the problem above and see if you can answer it on your own. Try not to peek below.

We can solve the problem above by listing all the possible sums of the number of dots. Rolling a 2 (that is, getting a sum of 2 from the top faces), for example, can be obtained by rolling a 1 from both dice.

To distinguish the difference, we assume that the two dice have different colors, say, red and blue.   It is clear that there is more than one way roll a 7, for instance 5 and 2, and 3 and 4.

To give us all the possible sums (or outcomes) of the two dice rolled, we construct an addition table of the number of dots as shown below. Using the table, we can observe the following:

1. There are 36 possible sums or outcomes.
2. The minimum sum is 2 and the maximum sum is 12.
3. The number of ways of getting a particular sum differs. For instance, there is only one way to roll a 2 (1 + 1), while there are three possible ways to roll a 4 (1 + 3, 2 + 2, 1+ 3).

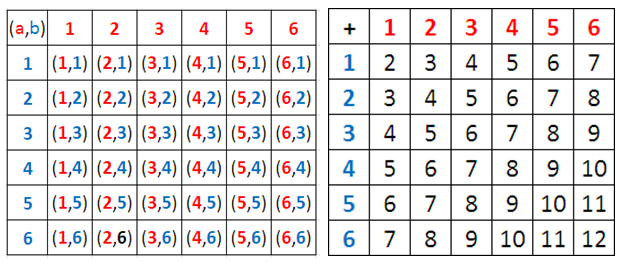
From the discussion above, we can therefore conclude that the probability rolling a 2 is 1/36 and the probability rolling a 4 is 3/36. We can also see that the best bet among the numbers is 7 (Why?). This means that if you toss the dice 36 times, it likely that you it will get a chance of getting a sum of 2 one time, and getting a sum of 4 three times.

From the second table, it is clear that number of possible outcomes is 36 and the probability rolling an even number is 1 + 3 + 5 + 5 + 3 + 1 = 18 out of 36.  Also, the probability of rolling an odd number is 2 + 4 + 6 + 4 + 2 = 18 out of 36 possible odd number outcomes. Therefore, Ishi is correct: The dice deal is fair.

From the table, we can see that the probability of rolling a 2 is 1 out of 36, which is equal to the probability of rolling a 12.

Application

The casino never cheats (hopefully), but all the games in the casino are designed to the house’s favor by means of probability, theoretical probability in particular (we will talk about it later in the series). For instance, if a casino will design a 2-die tossing game just like what Isha and Ishi  did, it will simply design the game to the its favor.  One possible scenario would be the following:

Casino wins if the sum of the number dots of the two dice is one of the following: 3, 6, 7, 8, and 11.

Players win if the sum of the number dots of the two dice is one of the following: 2, 4, 5, 9, 10, or 12.

At first glance, it seems that the player may think that he will win because he has six choices, and five only for the house (the casino), but the truth is the house has a greater chance of winning.

As we can see, the probability of getting sums of 3, 6, 7, 8, or 11 are 2/36, 5/36, 6/36, 5/36, and 2/36 respectively, which totals to 20/36. On the other hand, the probabilities of getting sums of 2, 4, 5, 9, 10, or 12 are 1/36, 3/36, 4/36, 4/36, 4/36, and 1/36 respectively, which only totals to 16/36.  This means that if the player play thirty 36 times, it is likely that the casino will win 20 times while the player will only win 16 times.

The probability that we have talked about above is called theoretical probability.  This means, that in principle, if we play  the casino’s die game  36 times, we can predict that the casino will win 20 times, but surely there is  no way of saying exactly how many. The probability 20/36 is just theory, but as we increase our number of events, we are certain that the result will be closer to that ratio.

Exercise: Devise a way to design a 2-die tossing game that gives the casino the maximum profit, while giving the player the 6 possible sums and the casino 5 possible sums.

Photos: Issa and Ishi, Transparency Demonstration (Dice) by Wikimedia Commons, Spin by Connor Withonen