Demystifying Triangle Inequality
This is the first part of the Triangle Inequality Series.
***
Given three segments, how are we sure that they will form a triangle?
Will the segments with lengths 3, 4, and 8 units form a triangle? What about 3, 5, and 8?
What conditions with respect to segment lengths must be satisfied, so that three segments form a triangle?
Shown below are the segments with lengths 3, 4 and 8 units. In the following illustrations, squares are used to clearly indicate the segments’ lengths. Each square has side 1 unit. As we can see, we cannot form a triangle if the sum of the lengths of the two sides is less than the third side.
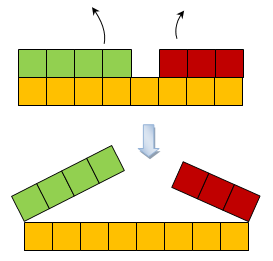
Figure 1
Let us now examine a triangle with side lengths 3, 5, and 8 units. Referring to Figure 2, the sides will only be coinciding and will never meet when rotated outward as shown.

Figure 2
If the sum of the lengths of the two sides is greater than the third side, then a triangle can be formed as shown in Figure 3.
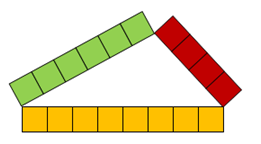
Figure 3
In general, to form a triangle using three segments, the sum of the two side lengths must be greater than the third side length. If the triangle has side lengths a, b and c, the following conditions must be satisfied: (1) a + b > c, (2) b + c > a, and (3) a + c > b. This theorem is called triangle inequality.
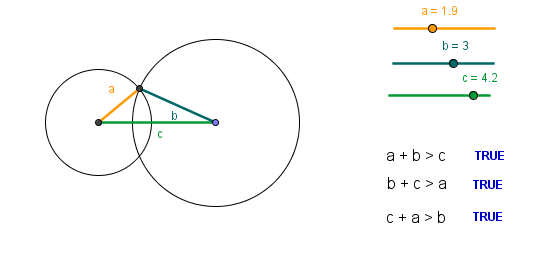
Generally speaking, triangle inequality states that the length of the two sides of a triangle should always be greater than length of the third side. Click the picture below to explore the GeoGebra applet about triangle inequality. Update: David Travis has an excellent applet modeled from the drawings above.
Exercise: A triangle has side lengths 5, 7, x. Find all the possible integral values of x.
To be concluded.