Young Gauss and the sum of the first n positive integers
Carl Friedrich Gauss was one of the most prolific mathematicians of all time. In fact, he was considered by many as the “Prince of Mathematicians” because of his numerous contributions in different fields of mathematics.
Gauss displayed his genius at an early age. According to anecdotes, when he was in primary school, he was punished by his teacher due to misbehavior. He was told to add the numbers from 1 to 100. He was able to compute its sum, which is 5050, in a matter of seconds.

Old Gauss
Now, how on earth did he do it?
Well, let’s have a few examples. Since it is very hard to add 100 numbers at once, we start with smaller numbers and see if we can see a pattern.
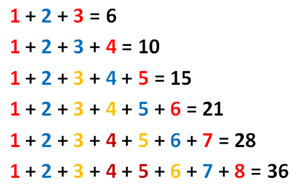
First, we observe that when the largest number is even, we can pair the numbers with the same color; that is, the last term and the first, the second and the second to the last terms, the third and the third to the last terms and so on, without a term left unpaired. In adding numbers from 1 through 6, for instance, it is clear that we have 6/2 or 3 pairs.
Second, we observe that if we add the terms mentioned above, the sum of each pair is always equal to the same number. For example, in adding a number from 1 through 6, we have (1 + 6), (2 + 5) and (3 + 4), which all equals to 6 + 1, and we know that 6 is the largest number.
From above, we have 3 pairs of numbers, each of which has a sum of 7. Therefore, the sum of the numbers from 1 through 6 maybe expressed as (6/2)(6+1) = 3(7) = 21. Now try a few examples and see if our the pattern holds.
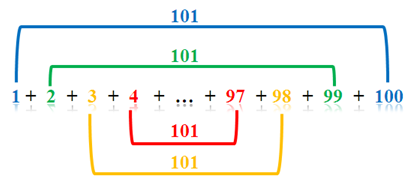
If we use this pattern, we can easily add the number from 1 through 100. We have the following pairs: (1 + 100), (2 +99), (3 + 98) and so on (see figure below). That is, we have 100/2 pairs of numbers, each of which, has a sum of (100 + 1). Therefore, we have (100/2)(100+1) = 50(101) = 5050. This was the strategy used by the young Gauss.
Now, let us generalize the pattern. What if we add the number from 1 through any number n? That is, what is the sum of
![]()
Well, if we add the first term and the second term, we have (1 + n), (2 + (n-1)), (3 + (n-2)), and so on.
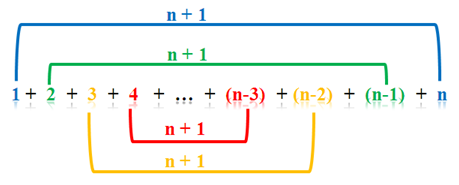
Notice that each pair has a sum of n + 1, and we have n/2 pairs of them. Therefore, the sum of all the integers from through
, or the first
positive integers is equal to
.
Exercise: Notice that the example was specified the first positive integers whose largest term is even. Explain why or why not the generalization will work if the largest integer is odd.
Another strategy
Another strategy is to let be the sum of the first
integers and then adding another
whose order of the sum expression is reversed.
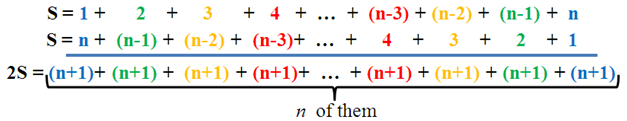
From the equation above, . Therefore,
. This is similar to our answer above.
Now our conjecture is that the sum of the first n positive integers is equal to .
How do we prove this? We need the proof of mathematical induction.
______
Credit: Photo of Gauss by Wikimedia Commons