Using Mathematics to Win the Lottery

Note: Prices and exchange rate discussed in this article are based on the time this article was written. They may change  in the near future.

Lottery Basics

Many of you are probably familiar how lottery works.  A lottery is a game where a smaller group of numbers is chosen from a larger group. If you bet on the right combination, you win the jackpot prize, which is usually staggering.

Since I am not familiar with lottery in other countries, I will use ours as an example. In the Philippines, as of this writing, we have three types of lottery: 6/42, 6/45 and 6/49. Yes, you guessed it right, 6/42 means 6 numbers are randomly chosen from a set of numbers from 1 through 42. We will use the 6/42 lottery in our discussion.

In our country, the process of how numbers are drawn is shown on television.  First, they place balls of the same weight numbered from 1 through 42 in a machine-operated transparent container. Next, they mix the balls using a blower located at the bottom of the container. These balls are light enough to be floated by the air from the blower. Finally to determine the winning combination, a button is pushed to eject 6 balls, one after the other. See video below.

Now, suppose we bought a ticket of the 6/42 lottery, what is our chance of winning? Is there a way that we can win for sure?

We will answer the first question later. For the second question, yes, there is a way and, in principle, it’s simple. Just bet on all the possible number combinations.

Okay, so you’re not a math major and you do not know what I am talking about. Well, let me explain it in plain language.   Suppose a mini-lottery has 5 numbers, say 1 through 5, and two numbers are drawn to determine the winner. The pair, {1,2} is a possible bet as well as {4,3}.  It is clear that the order of the numbers chosen does not matter, so betting on {5,2} is the same as betting on {2,5}.

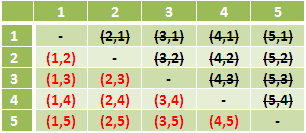
Finding all the possible pairs or combinations in the 2/5 mini-lottery is a bit easy.  As we can see from the table, if we choose two numbers from 5 choices, we have 10 possible combinations or pairs (see red text). The pairs in black texts are just the reverse of those in red.  We did not also include the pair having the same number, say (2,2), because in a lottery draw, ejected balls are not returned back into the container before drawing the next ball.

If we buy 10 tickets and bet on all the 10 pairs on the table, surely, we will win. We will use the same principle in winning the 6/42 lottery draw.

Systematic Betting

Now it is very hard to use the strategy above if we have six numbers taken from 42.  There is no easy way to tally our bets.  However, we can use a computer in finding all the possible number combinations. The method below maybe done:

1. We can start with 1,2,3,4,5,6, then 1,2,3,4,5, 7, and then 1,2,3,4,5,6,8 all the way up to 1, 2, 3, 4, 5, 42.
2. After that, we can increase the fifth digit by 1 and we start with 1, 2, 3, 4, 6, 7, and then 1, 2, 3, 4, 6, 8, and so on. We can do this all the way to 1, 2, 3, 4, 6, 42.
3. When our sixth digit reached 42, we now increase the fifth digit by 1; that is, 1, 2, 3, 4, 7, 8; 1, 2, 3, 4, 7, 9 all the way up to 1, 2, 3, 4, 5, 7, 42.
4. Every time we increase the fifth digit by 1, we get the sixth digit by adding the fifth digit by 1, and then keep adding 1 until the sixth digit reached 42. For instance, 1, 2, 3, 4, 8, 9; 1, 2, 3, 4, 8, 10 all the way up to 1, 2, 3, 4, 8, 42. In varying the fifth digit, our last number would be 1, 2, 3, 4, 41, 42.
5. After the last combination is finished, we change the third digit: 1, 2, 4, 5, 6,  7 and so on…

Exercise:

Another mini-lottery has 5 balls and 3 balls to be drawn. List all the possible combinations. How many tickets should we buy for a sure win?

Winning the 6/42 lottery

In the 2/5 mini-lottery example above, we have two numbers chosen from a group of 5 numbers. This is equivalent to the combination of 5 numbers taken 2 at time.  We have learned from the Introduction to Combination post that 5 taken 2 at a time is equal to , and that can be verified from our table above. In the 6/42 lottery, 42 taken 6 is equal to .  This means if we want a sure win, we must buy 5,245,786 tickets.

The Constraints of Winning

There are, however, several constraints in getting our fortune and becoming a millionaire, although it is definitely possible. Some of them are enumerated below.

1. Ticket Price.One 6/42 lottery ticket is 10 pesos. This means that we will need 52,457,860 pesos (about 1,165,000 US dollars) to buy all the
   

   Hmmm... Are you sure we will win?

   tickets.

2. Buying and Filling Out Tickets. Assuming that we have the money, we also have a problem where to buy 5 million tickets. Suppose that luck is on our side and 100 lottery outlets in our place have 5 million tickets, how long will it take us to fill them out?
3. Number Combinations. We should also have a way of organizing our number combinations. Note that in the five million plus tickets, we must fill out our numbers accurately and without duplicates. The mini-lottery above can be easily listed, but we will need a computer program to enumerate the 5,245,786 combinations. Well, we can definitely afford a programmer since we are ready to spend more than 50 million pesos.
4. Prize money. Needless to say, if we want to spend 52 million pesos, the jackpot prize should be more than that.
5. More than 1 Jackpot prize winners. Even if the prize money is more than 50 million, we still have one problem.  If another person wins, we are in big trouble.  If the jackpot prize, for instance, is 100 million pesos, and there are three winners, each of the winners will only bag 33 million pesos, and we are 19 million pesos short.

Now, you probably understand why many mathematicians do not bother to buy lottery tickets, despite the fact that they know how to win. The answer to our second question above is that the chance of winning is 1 in 5,245,786.

What does that mean?

That means that if you buy a single 6-42 ticket and bet randomly 5,245,786 times, it is likely that you will win only once.

But why there’s always a winner every draw?

Millions of people bet on lottery in each draw, so it is likely, that one or more would win. If 2 million people bet different combinations in one draw, that is equivalent to one person betting 2 million times.

It has been done

Despite the numerous constraints, in 1995(?), two computer scientists from United States flew to Australia just to bet on a lottery (I saw the documentary several years ago).  They used a computer to systematically bet on all combinations. One lottery outlet was surprised when they told them that they were going to buy 100,000 tickets. The problem was they didn’t have enough tickets, so they have not bet on all possible number combinations.

They won anyway.

Final Note: There is no secret to win a lottery. The only secret to increase your chance of winning is to buy more tickets. The more tickets you buy, the higher your chance of winning. In the 6-42 lottery above, if you are going to buy 2, 622, 893 tickets, then you have a 50% chance of winning.

***

I am not really sure the process of lottery betting done in other countries, but here, first we buy tickets, then fill up our numbers of choice, then return it to the lottery outlet for processing. They place the ticket in a machine, and the machine ejects the receipt containing our number combinations. The receipt will be our official ticket.

Photos: Money by AMagill, The Thinker by Andrew Horne