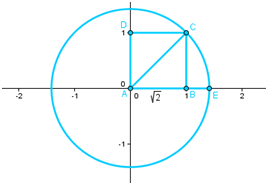
Constructing segments with irrational lengths
Since rational numbers can be expressed as fractions (or ratio of two integers), rational numbers can be easily located on the number line using compass and straightedge construction. In principle, a segment of any length can be divided into any number of parts; hence, it is possible to locate any rational number on the number line. Irrational numbers, on the other hand, cannot be expressed as ratio of two integers, so the big question is:
How do we locate irrational numbers on the number line?
The question above is equivalent to: “How do we construct a segment with irrational lengths?”
It is easy to locate some irrational numbers on the number line even with compass and straightedge construction. The irrational can be located by constructing square ABCD (Figure 1), getting the diagonal AC, and constructing a circle with radius AC. It follows that the length of AE is
, and the coordinates point E are
.
It is also apparent that the easiest way to construct segments with irrational lengths is by constructing diagonals of rectangles. In Figure 2, OB, OC and OD have lengths ,
, and
respectively. More complicated construction is required to construct other irrational lengths,
for instance, which is the length of EH.

Figure 2
Exercise: Explain why the length of EH is equal to .
Algebraically, if we let be the diagonal of the square ABCD in Figure 1, then by the Pythagorean Theorem, we get
, which is equivalent to
. Now, note that getting the value of
in
is the same as getting the root of the function
. Therefore, it is possible to locate an irrational number on the number line by getting the root of a function, or, equivalently, graphing function and finding its x-intercept. The following is an example:
Suppose we want to locate the position of the irrational number on the number line. Here’s what we should do: First let
. Multiplying both sides by
, we have
. Now, squaring both sides we have
. Simplifying we have
. Now, if we locate the the positive root of
, we now locate the coordinates of
; thus, we now know the length
.
Exercise: Give the equation of the function with root .
There is one thing that we can observe about the polynomial above. The numerical coefficients of the terms are integers. Irrational numbers that can be generated as roots of polynomials with integral –rational to be exact — coefficients are called algebraic numbers; those which cannot be are called transcendental numbers.
The numbers ,
and
, where
less than 1000 (where
is not equal to 1, 10, 100 or 1000) are all transcendental numbers.
Geometrically, it is impossible to construct “transcendental lengths” using compass and straightedge.
We will talk about algebraic and transcendental numbers in the future.