Eratosthenes and the Earth’s Circumference
Eratosthenes was one of the most famous mathematicians in the early times. He was famous for his sieve – a strategy for finding prime numbers – but one of his greatest achievements was estimating the circumference of the earth. In this post, we learn how Eratosthenes used mathematics to solve the size of the earth. We leave out some of the technical details (such that the assumption that the sun is so far away that its rays are almost parallel), since this post is for elementary school mathematics students.
How did he do it?
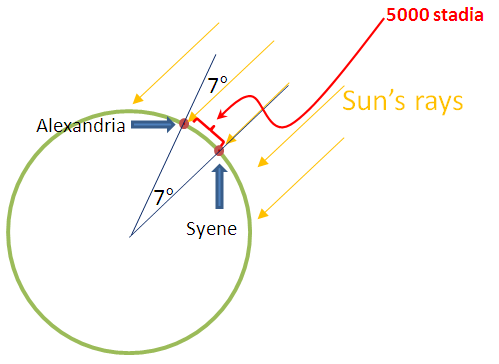
Eratosthenes knew that at noon in Syene, the sun casts no shadows. This can be tested using a sundial – a device used to tell the time using its shadow during the ancient time.

At the same time, he observed that in Alexandria, his hometown, the angle of elevation of sun’s rays at noon is about 7 degrees. Now, the distance from Syene to Alexandria is about 5000 stadia (an ancient unit of measurement and plural of stadion). This means that 1 degree is equal to about 714 stadia. To compute, since a circle is 360 degrees, we multiply 714 by 360 giving us the circumference of the earth which is about 257,040 stadia.
In ancient measurement, there are two types of stadia measurements. The Attic stadion about 186 meters while the Egyptian stadion is 157 meters. If Eratosthenes used the Attic stadion, then the circumference of the earth, based on his measurement, is about 47,809 kilometers, about 18% larger than the actual circumference of the earth which is 40,075 kilometers. However, if Eratosthenes used the Egyptian stadion, we multiply 257,040 stadia by 157 meters and divide it by 1000 meters (since 1000 meters = 1 kilometer) we have 40,355 kilometers, which has an error of about 280 kilometers. Now, that error is less than one percent of earth’s size.
Photo Credit: Sundial from Wikipedia