Demystifying Degree and Radian Measures

Introduction

We have learned about angle measures since elementary grades. In Figure 1, we have a circle with center A, and radius length 1. Angle CAB measures 90 degrees and intercepting minor arc BC. This is also the same as saying that arc BC is subtending angle CAB. We have also learned that the entire rotation about the center of a circle is 360 degrees.

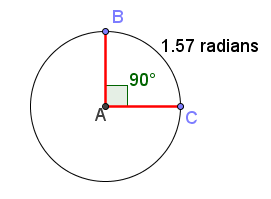
Another unit of angle measure besides degree is radian. Now, what is radian? How is it related to degree?

Consider the second figure shown below. Segment OP is the radius of the circle with center O, and NP is the arc subtending angle NOP. If NP is a string that wraps the portion of a circle, if we “straightened” it and its length equals the length of OP, then we say that angle NOP is equal to one radian. Therefore,

One radian is equal to the angle measure at the center of a circle subtended by an arc equal in length to the radius.

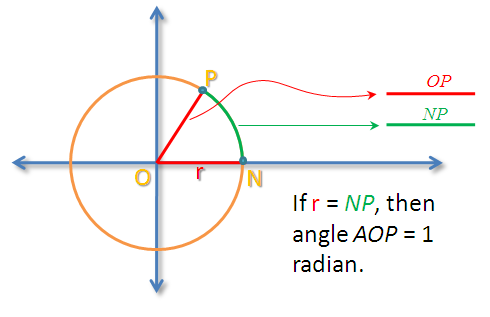
If the length of NP = r, then how many radians is the entire rotation of point P about the center O?

We know that the circumference of the circle equals $katex 2 \pi r$. Note that angle NOP, which intercepts arc NP, equals 1 radian. Now, we are looking for x, which intercepts the circumference of the circle. Thus, we have the following ratio: angle NOP : radius length = x : circumference of the circle. But angle NOP is equal to 1 radian and the circumference of the circle is equal to $2 \pi r$ . Substituting we have

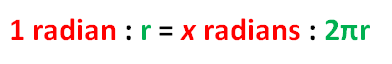
Now, the ratio above is the same as $\displaystyle\frac{1}{r} =\frac{x}{2 \pi r}$ . Solving for $x$ , we have $x = 2 \pi$ . This means that the entire rotation about the circle is equal to $2 \pi$ radians.

We have mentioned that the rotation about the center of a circle is 360 degrees. Therefore, $2 \pi$ radians = $360$ degrees. or equivalently, $\pi$ radians $180$ degrees. These are the only equations that we should remember especially when converting degree to radian measure and vice versa.

Conversion

To give us a feel of the worth of our discussion above, let us have a few examples on degree-radian conversions. We will use ratio and proportion to convert degrees to radian and vice versa.

Example 1: Convert $120$ to radians.

Solution: We go back to what we know: $\pi$ radians = $180$ degrees. Now, let’s use ratio and proportion: $\pi : 180 = x : 135$ . It follows that $180x = 120 \pi$ . Dividing both sides by 180, we have $\displaystyle\frac{2 \pi}{3}$ . Hence, 120 degrees equals $\displaystyle\frac{2 \pi}{3}$ radians.

Example 2: Convert $\displaystyle\frac{3 \pi}{4}$ to degrees.

Solution: Let y be the measure of $\displaystyle\frac{3 \pi}{4}$ in radians. Again, using ratio and proportion, we have $\pi : 180 = \displaystyle\frac{3 \pi}{4} : y$ . Solving, we have $y = 135$ degrees.

As you can see, you don’t really have to memorize which to multiply, $\displaystyle\frac{\pi}{180}$ or $\displaystyle\frac{180}{\pi}$ in conversion.

Generalization

Of course, we can generalize the situation above. For instance $\pi : 180 = x : a$ where $a$ is the given degree measure. Solving we have $x = a (\displaystyle\frac{\pi}{180})$ . That’s the reason why you multiply the degree measure by $\displaystyle\frac{\pi}{180}$ when converting degree to radian measure. But as I have said earlier, no need to memorize. Just use ratio and proportion.

Exercise: Show the derivation of converting radian to degree measure.

*Multiplying the mean, which are the two inner numbers and the extremes, which are the two outer numbers. This is valid because $a:b = c:d$ means, $\displaystyle\frac{a}{b} = \frac{c}{d}$ . Therefore, $ad = bc$ .