The Seven Bridges of Königsberg

The city of  Königsberg, Prussia (now Kaliningrad, Russia) was set on both sides of the Pregel river.  There were two islands on the river and there were seven bridges connecting them and the main land as shown in Figure 1.

Residents observed that using the bridge at the southern part of the city (Bridge 1 in Figure 2) as starting point, they could not stroll around crossing all the bridges only once. They had to skip one bridge or cross some bridges twice. Some of them conjectured that it was impossible to cross the seven bridges once and only once, but they could not explain why. 

The problem was submitted to the great  Leonard Euler, one of the most famous mathematicians that time.  Euler proved that there was no solution to the problem; that is, there was no way to cross the seven bridges exactly once.

The Proof

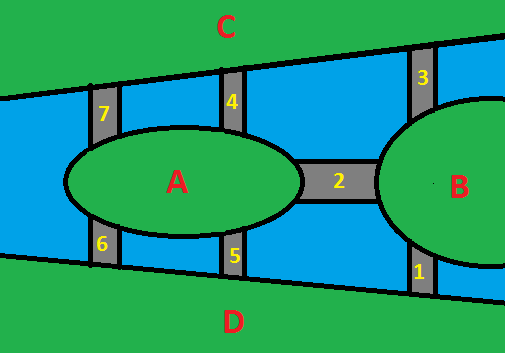
To showcase my talent on using Paintbrush, I created my own rendition of Konigsberg below (chuckles). The blue parts represent the river, the green parts represent the lands, and the gray parts represent the bridges. For the sake of discussion, I have also labeled the land masses and the bridges.

Since island B is less complicated, we will discuss it first.

Case 1: Starting OFF Island B

There are three bridges leading to island B. If we start elsewhere (A, D, or C), to use each of the three bridges only once,  we have to come to the island using the first bridge (ON), leave the island using the second bridge (OFF), and then come back to the island using the third bridge (ON). Notice that the order of crossing bridges, or the starting point does not matter. The ON-OFF-ON notation tells us that we would end up ON the island. We proved our first theorem.

Theorem 1: If we started OFF  island B, we would end ON island B.

Case 2: Starting OFF Island A

There are five bridges leading to island A. If we start elsewhere (B, C, or D), we come to the island using the first bridge (ON), leave the island using the second bridge(OFF), come back using the third bridge (ON), leave again using the fourth bridge (OFF), and come back again using the fifth bridge (ON). Again,  the order of crossing bridges, or the starting point does not matter. The ON-OFF-ON-OFF-ON notation tells us that we would end up ON the island. We have proved our second theorem.

Theorem 2: If we started OFF  island A, we would end ON  island A.

Back to the Problem

As the problem requires, our starting point is D, using bridge 1 to enter island B. But using this condition implies that we will both satisfy  Case 1 and Case 2 (Can you see why?). But we cannot end up ON island A and ON island B at the same time. Therefore, crossing the seven bridges exactly once is impossible.

The problem and the proof above resulted to a new kind of mathematics we now call graph theory. Graph theory has a lot of applications in computer science particularly in web and network technology.