The Marvels of the Nine-Point Circle
Let us examine some important points related to a triangle. Use GeoGebra or any geometry software to follow the construction below.
1.) Construct triangle TUV.
2.) Construct the midpoint of each side.
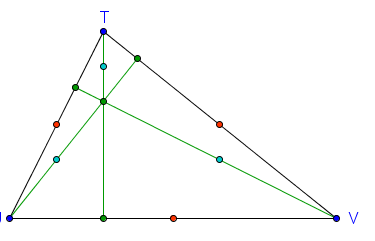
3.) Construct the three altitudes. What do you observe? The intersection of the altitudes is called the orthocenter.
4.) Construct the three midpoints between the orthocenter and the three vertices. What do you observe about the nine points?
After finishing the steps above, your figure should at look like Figure 1. For the sake of discussion, we color the points. The red points are the midpoints of each side, the green points are the ‘foot’ of each altitude, and the cyan points are the midpoints of the orthocenter and and the vertices.
From the figure above, we observe two things: first, the altitudes seem to meet at a point; and second, it seems that the 9 points form a circle (can you verify this by construction?).
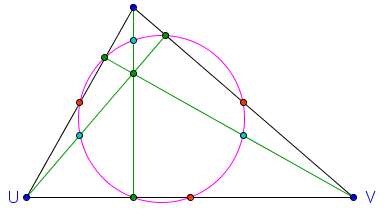
Using GeoGebra, we can verify if the nine points mentioned above lie on a circle. To do this, just select the Circle through Three Points tool, and then click any three of the nine points.
As we can see, the nine points are indeed on a circle . The circle is what we call the nine-point circle.
We find other interesting points on the circle.
5.) We construct a circumcircle –– a circle passing through vertices of the triangle and find its circumcenter (the center of the circumcircle). What can you say about the orthocenter, the center of the nine-point circle, and the circumcenter?
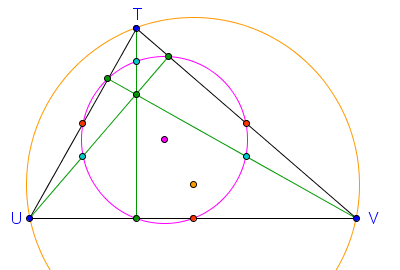
6.) We draw the medians — the segments that connect the three vertices to the midpoint of each side. What do you observe?
7.) We construct the centroid — the intersection of the medians.What do you observe?
- The center of the nine-point circle is the midpoint of the orthocenter and the circumcenter.
- The radius of the circumcircle is twice that of the nine-point circle
- The incircle of a triangle is always inscribled to its nine-point circle.