The Handshake Problem and Its Multiple Solutions
Introduction
We teach mathematics in order to elicit thinking among students. Choosing ‘rich’ problems can give students opportunities to think and discuss among their peers.
Rich problems are challenging tasks that have many solutions and/or many answers. Giving students these kind of problem will encourage them to explore, and evaluate which solutions best fit. It is also important that we train them to solve problems in as many ways as they can.
The problem below is an example of such task. Only four solutions are written, but I assure you that there’s more.
Problem
In a wedding reception, guests were seated around a circular table for six. Before the dinner, the newlywed asked each guest to shake hands (once) with everyone on the table. How many handshakes were made in each table?
Solutions
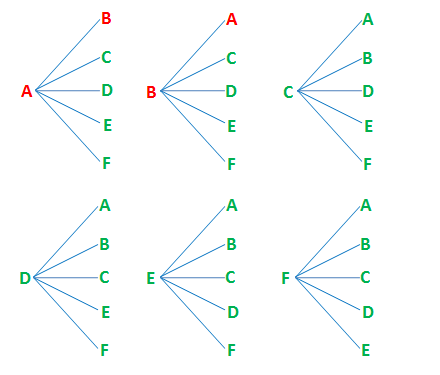
Solution 1: We represent the 6 visitors in each table by letters A, B, C, D, E and F. We use the tree diagram as shown in the first figure to represent handhsakes. Person A handshakes with each persons on the table: persons B, C, D, E, and F. These handshakes are represented by segments. Person B handshakes with persons A, C, D, E, and F. But a handshake between person A and B is the same as the handshake of B and A (see red letters). Therefore, each handshake was counted twice.
The figure above shows that there are 30 handshakes in a table, but since we have counted the handshakes twice, we divide the total number of handshakes by 2. This gives us 15 handshakes.
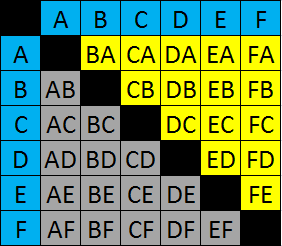
Solution 2: We use a table to exhaust the number of handshakes. Each person do not have to handshake with himself, so we put the black diagonal. We represent the handshake by naming the person in the column first, and then the row as shown in the third figure. So column B and row A is handshake BA.We now construct all the possible handshakes.
Notice that the handshakes in the yellow part of the table are repeated in the gray part with the order of the representation reversed; that is, FE in the yellow cell, and EF is the gray cell. Since handshake EF is the same as handshake FE, to determine the number of handshakes, we just count the yellow-colored cell (or the handshakes in the gray-colored cells). By counting the cells, we see that there are only 15 handshakes.
Solution 3: A geometric representation may also be used to solve the problem. The handshake problem is equivalent to finding the number of segments that connect six non-collinear points.
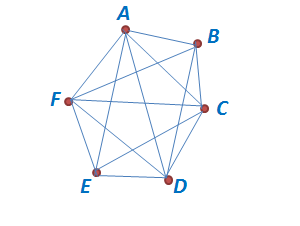 In this solution, it is easy to count the segments, which is equivalent to the handshakes. It is clear that there are 15 handshakes.
In this solution, it is easy to count the segments, which is equivalent to the handshakes. It is clear that there are 15 handshakes.
Solution 4: There are six persons in a table, each of whom, will handshake the other five. Therefore there are 30 handshakes. However, the handshake of person A and person B is the same as the handshake of person B and person A. Therefore, we have counted the handshakes twice. Hence, there are only 15 handshakes that happened.
Exercise: Using the method above, investigate the number of handshakes, and find the formula for the number of handshakes that can be done given any number of guests in a table.