The Complements Theorem

High School Mathematics, High School Trigonometry

In this post, we discuss the proof behind one of the most commonly used identities in trigonometry. We examine the equations below and  show why the relationships always hold.

\sin \theta = \cos (90^{\circ} - \theta)
\cos \theta = \sin(90^{\circ} - \theta)

To students who have taken trigonometry, I’m sure that you have met these equation before.  The proof of these equations are as follows.

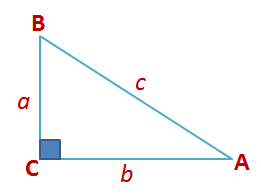
Consider triangle ABC right angled at C. From the definitions, we know that

\sin A = \displaystyle\frac{a}{c}
\cos A = \displaystyle\frac{b}{c}
\sin B = \displaystyle\frac{b}{c}
\cos B = \displaystyle\frac{a}{c}

 Therefore, (1) \sin A = \cos B and (2) \cos A = \sin B.

Now, If we let A = \theta, then B = 90^{\circ} - \theta, then substituting the values of A and B in (1) and (2), we have

\sin \theta = \cos (90^{\circ} - \theta)
\cos \theta = \sin (90^{\circ} - \theta)

 and these are what we want to show.

As exercises, use the strategy above, or any strategy you want to prove the following identities.

1.) \cot\theta = \tan (90^{\circ} - \theta)
2.) \sec \theta = \csc(90^{\circ} - \theta)

2 comments , ,

Leave a Reply