Understanding the Meaning of Discriminant
In the Derivation of the Quadratic Formula, we have learned that the solutions to the quadratic equation , where
, is described by the equation
.
Graphically, getting the solutions of is equivalent to getting the value of
when
of the function
,
. This means that the quadratic formula above describes the root of the quadratic function
.
From the equation, the indicates that the quadratic polynomial can have at most two roots, depending on the value of the expression under the radical sign. That is, the roots of the quadratic polyonomials are
and
.
The number of roots, however, will depend on the expression . Notice that if it is negative, there is no root (real root to be exact), since we cannot extract the square root of a negative number. Therefore, if
, then, there is no real root.
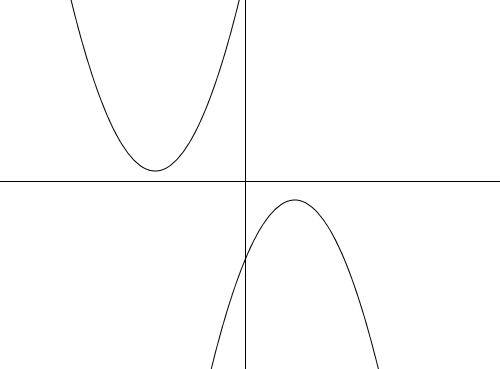
Geometrically, the root is the x-value of the function when y is 0, or where the function crosses the x-axis. Hence, if there is no real root, the graph of the quadratic function does not cross the x-axis (see first figure). The examples of these quadratic functions are shown above. Both quadratic functions have no real roots.
The second case is if is 0. This means that
.
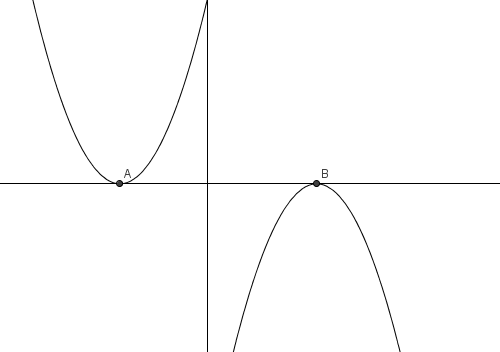
Hence, we only have one root which equals to . Since the quadratic function has only one root, it crosses the x-axis only once. The sample graphs of this case are shown in the second figure. Each of the two quadratic functions has one root, the first one represented by A, and the second is represented by B.
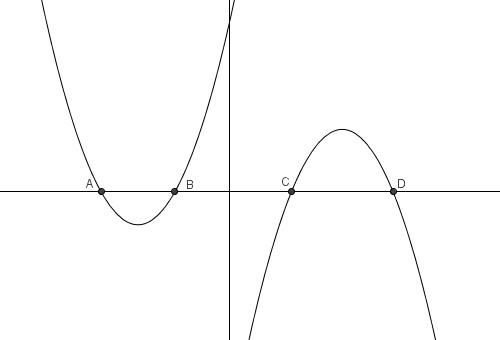
The third case is, of course, if . This gives us two roots as we have mentioned above. The graph of the quadratic functions with two roots are shown below.
The expression is called the discriminant of the quadratic polynomial. In general, the discriminant of a polynomial gives information about the nature of the polynomial’s roots.