This is the 9th tutorial of the GeoGebra Basic Geometric Construction Series – a series about constructing and drawing basic geometric figures using GeoGebra.

In this post, we learn how to construct a kite. A kite is geometric figure whose four sides can be grouped into two pairs of equal-length sides that are next to each other. Follow the instructions below to construct the kite.
Step by Step Instructions
|
1.) Open GeoGebra and select Geometry from the Perspective menu. |
|
2.) We also want all created points to have labels so that we can refer to them easily. To do this, select Options>Labeling> New Points Only from the menu bar. |
 |
3.) First we create ray AB. Select the Ray through Two Points tool and click two different locations on the Graphics view to construct ray AB. |
 |
4.) Select the Circle with Center through Point, click point B and then click point A to construct a circle with center B and passing through A. |
 |
5.) Now, select the New Point tool and click the intersection of the circle and ray to construct point C. Your drawing should look like Figure 1.
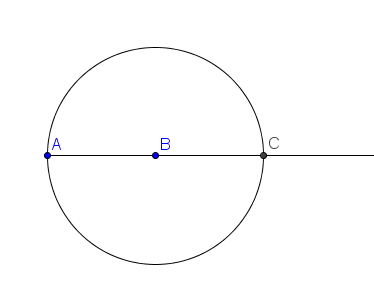 Figure 1
|
 |
6.) Use the New Point tool to construct D on the circle. |
 |
7.) Next, we will reflect D about ray AC. To do this, select the Reflect Object About Line tool, click D, and then click ray AC (click the ray, not the points). Notice that point D’, the reflection of D about ray AC, appears on the circle. |
 |
8.) Use the Segment between Two Points tool to construct segments AD, AD‘, CD, and CD‘. After this step, your construction should look like Figure 2.
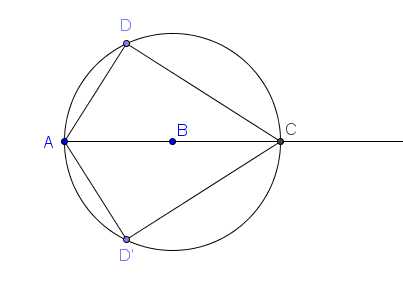
|
|
9.) To finish, hide the circle and the ray by right clicking them and then clicking Show label from the context menu. |
 |
10.) Move points A, B, or C. Does the figure remain a kite? Why? |
Challenge: Think of other ways of constructing a kite using GeoGebra.


