Diagonals of a Parallelogram

Coordinate geometry was one of the greatest inventions in mathematics.  Aside from connecting geometry and algebra, it has made many geometric proofs short and easy.  In the example below, we use coordinate geometry to prove that the diagonals of a parallelogram bisect each other.

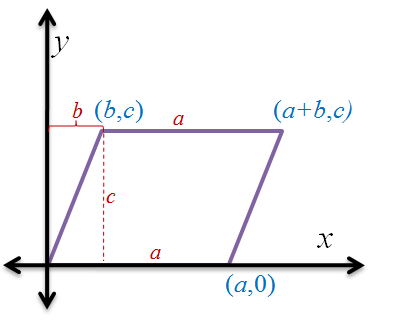
The proof can be simplified by placing a vertex of the parallelogram at the origin and one side coinciding with the x-axis.  If we let a and b be the side lengths of the parallelogram and c as its altitude, then, the coordinates of the vertices can be easily determined as shown below.

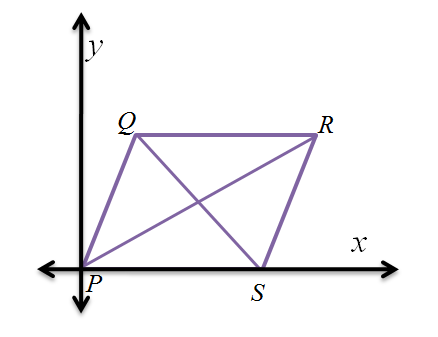
In addition, if we label the vertices P, Q, R, and S starting from the origin and going clockwise, then the coordinates of the vertices are P(0,0), Q(b,c), R(a + b,c) and S(a,0).

To prove that the diagonals bisect each other, we have to show that they have the same midpoint; that is, we have to show that their midpoints have the same coordinates.

Let be the midpoint of  PR, and be the midpoint of QS. Calculating for the midpoint, we have

and .

Since the midpoints of the diagonals have the same coordinates, the theorem is proved.

Note that this proof encompasses all types of parallelograms: rectangles, rhombuses (rhombi), and squares.