Using Paper Folding to Introduce the Notion of Proof
Two years ago, I worked as part-time geometry instructor in a technical school near our university. Most of the students in that school were quite clueless about the notion of proofs, so I tried to find ways to introduce proofs in an intuitive manner.
One lesson I developed was on proving that a quadrilateral formed from paper folding is a square. I let the students create a square from a piece of bond paper without using any measuring instrument; only folding and cutting were allowed.
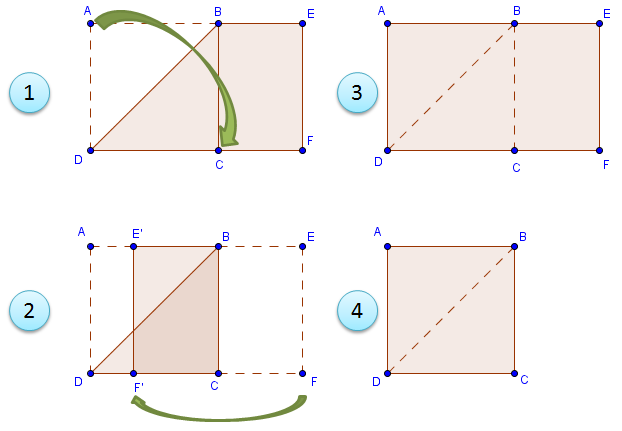
As expected, most of the students used the method shown in the figure above. For the sake of discussion, we label the corners and critical points of the bond paper. Most of the students constructed the square using the following steps (see figure):
- Fold the paper such that point A coincides with point C, and then crease well.
- Fold along BC by placing F on DC (represented by F’ in the figure).
- Unfold all.
- Cut along BC with a scissors.
Although the students had created a square, they had no idea how to explain why the final figure was a square. I asked them “What do we need to show to prove that this is a square?” After a few minutes of discussion, they had agreed that to show that the final figure is a square, they must show that (1) the interior angles measure 90˚ and (2) the four sides are congruent.
Through a series of questions I asked, the students realized the following:
- Angle A and angle ADC measure 90˚ since they are corners of the bond paper (the bond paper is a rectangle).
- Angle BCD is also 90˚, since when fold 1 was made, angle A coincided with angle BCD.
- Angle ABC measures 90˚ since when fold 1 was made, ADB coincided with angle BDC and each of which measure 45˚ (since segment DB divides angle ADC).
From these realizations, the students knew that it remained to be shown that the four sides of ABCD are congruent. Again, through a series of questions, they realized the following:
- AD is congruent to CD since they coincide when fold 1 was made. For the same reason, AB is congruent to BC .
- BC is congruent to CD since BCD is a 45˚-45˚-90˚ triangle.
- AD is congruent to AB is congruent because ABD is 45˚-45˚-90˚ triangle.
Although some properties discussed above implied other properties, they were not seen by most students. We had to prove them one by one. The last part of our lesson was to write the proof in paragraph form concisely.
I think those who are teaching geometry and introducing the concept of proofs should try out this lesson. I would love to hear what happened in your class.