The Mathematics of Leap Years Explained
Year 2016 is a leap year!. The years 2000, 2004, 2008 and 2012 are leap years too, so you probably see the pattern that the years divisible by 4 are leap years. Now, is this always true?
The answer is NO. The years 1900, 2100, 2200, and 2300 are divisible by 4, but they are not leap years. Uhm, are all years divisible by 100 not leap years?
The answer is still no. The years 1600, 2000 and 2400 are divisible by 100, but are leap years.
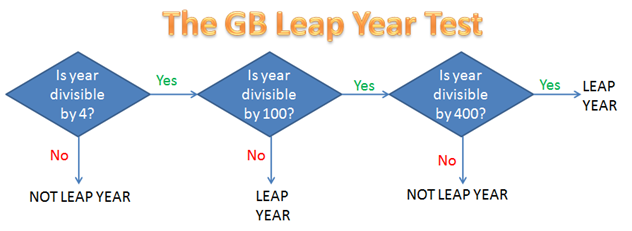
If you are a little bit confused, examine the GB Leap Year Test (wink) diagram below.
As we can see, if a year is divisible by 4 and not divisible by 100, then we are sure that it is a leap year. So, 1924, 1936, 2028 are leap years (Can you give four more examples?).
Now, if a year is divisible by 100, we are not sure if it is a leap year yet; we need to test if it is divisible by 400. If it is divisible by 400, then, it is a leap year, otherwise, it is not. So, 1700, 1800, and 1900 are not leap years, but 1600 and 2000 are leap years.
We can summarize the discussion above as follows.
- Years that are divisible by 4 and not divisible by 100 are leap years.
- Years that are divisible by 100 but not divisible by 400 are NOT leap years.
- Years that are divisible by 400 are leap years.
The Mathematics Behind the Complication
Why add one day?
If each year is exactly 365 days, then four years is exactly 1460 days. But that is not the case. A year is approximately 365 ¼ days. So,
365 ¼ days/year x 4 years = 1461 days.
As we can see, there are 1461 days in four years instead of 1460 days. That is the reason why we add a day every four years, which is the 29th of February.
What about the divisibility by 100 and 400?
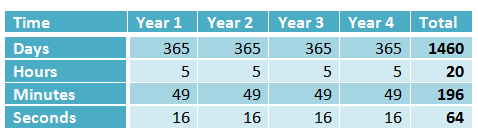
If a year is exactly 365 ¼ days (or 365 days and 6 hours), our trouble would be over. A year, however, is 365 days, 5 hours, 49 minutes, and 16 seconds (source: Dr. Meghan Gray, Nottingham).
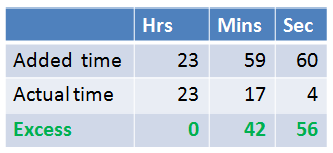
Looking at the table above, we can see that every four years, the time accumulated is 1460 days, 20 hours, 196 minutes, and 64 seconds; or 1460 days, 23 hours, 17 minutes, and 4 seconds instead of 1461. But adding February 29 is adding one full day (24 hours = 23 hours 59 minutes 60 seconds). In effect, we have an excess time of 42 minutes and 56 seconds every leap year.
Note that in a hundred years (25th leap year), the time accumulated will have been 17 hours 53 minutes and 20 seconds (multiply 42 minutes and 56 seconds by 25) or almost a day.
To adjust again, a day is taken away on the 100th year. That is the reason why years that are divisible by 100 (but not divisible by 400) are not leap years.
In taking a day every 25th leap year, we take away 24 hours instead of taking away 17 hours 53 minutes and 20 seconds. In effect, we have a deficiency of 6 hours, 6 minutes, and 40 seconds.
So in four hundred years, we would have taken 24 hours, 24 minutes, and 160 seconds (multiply 6 hours 6 minutes 40 seconds by 4) or 24 hours, 26 minutes, and 40 seconds. That is why, we add an extra day every 400 years, and that is the reason why years that are divisible by 400 are leap years.
Notice that these adjustments are still not accurate. We still have an excess time of 26 minutes and 40 seconds, so scientists and mathematicians will still re-adjust after several hundred years.