Constructing Open-Ended Math Problems
We communicate to students what we value through the questions we ask. If we ask them questions always require them to memorize, then we are implicitly telling them, that mathematics is a science of procedures and formulas. On the other hand, if ask them challenging questions, we are telling them that mathematics is about problem solving. In this post, we discuss these challenging questions — questions that are sometimes labeled as open-ended problems.
Open-ended math problems are problems with more than one correct solution and/or problems more than one correct answer. One of the benefits of asking this kind of questions is that it allows to explore more, even if they had already found the answer. Giving open-ended math problems sometimes results to rich discussions in the classroom.
In the examples below, we revise ordinary textbook problems to produce open-ended math problems. The examples are closed ended problems, while the revised examples are open-ended math problems.
Example 1: Numbers
Which of the following symbols goes into the blank: ———-
.
a. >
b. =
c. <
d. cannot be determined
Revised Example 1
- Write a fraction greater than
.
- Write a fraction that is greater than
but less than
.
Example 2: Algebra
Find the distance between and
.
Revised Example 2:
If is
units and the coordinates of
are
, find all the possible coordinates
of
if
and
are both integers.
Example 3: Geometry
In the figure below, find the area of triangle ABC.
Revised Example 3
The smallest square on the grid is 1 square unit. Using the grid*, draw a triangle with area 6.
Notice that there are more than one answer in each of the three revised questions above. Questions 1 and 3 have infinitely many answers, while question 2 has 12 answers. There are also questions, however, that has only one answer, but the challenge is finding as many solutions as possible. The next problem (Source: TIMSS 2003) is an example of such question.
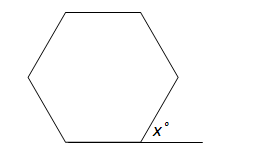
The figure below is a regular hexagon. Find the value of x in as many ways as you can.
We used this question in one of our research lessons in lesson study, and we have generated 16 solutions!
*Grid must be distributed with no drawings.