Why is negative times negative equals positive?
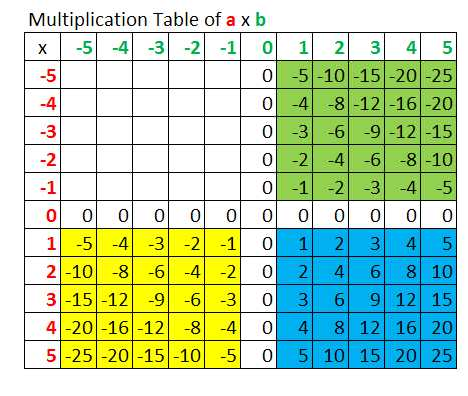
We have learned that the product of a positive number and a negative number is negative. How about the product of two negative numbers? How do we know that it is positive? Below are some illustrations and proof that show why is the product of two numbers positive.
Reason 1 – Pattern
Let us consider the pattern below.
From the patterns, it should be .
Reason 2 – Contradiction If Otherwise
Suppose the product of two negative numbers is negative. Then, (-2)(-3) = -6. Since the distributive property multiplication over addition holds,
-2 (-3 + 3) = -2(-3 + 3)
-2 (0) = (-2)(-3) + (-2)(3)
0= -6 + -6
0 = -12.
This is a contradiction!
The proof below requires elementary knowledge in algebra, so I have included it.
The Proof
Let and
be real numbers.
Define x = ab + (-a)(b) + (-a)(-b).
We factor out from x = ab + (-a)(b) + (-a)(-b):
.
. (1)
We now factor out from x = ab + (-a)(b) + (-a)(-b):
. (2)
Since (1) and (2) are equal, .
Therefore, the product of two negative numbers is positive.
Reference: Ask Dr. Math