Understanding If Then Statements and Counterexamples
If then statements are common in everyday conversations. If mom is going home this holiday season, then we are going to have a grand celebration. If you pass the exam, then I’m going to buy you a tablet. But how is if then statements related to mathematics?
If then statements can be seen in almost every field of mathematics. They are mostly found in mathematical proofs. You will have to familiarize yourself with its structure if you are going to be a mathematics major in the future.
In the statement “if a polygon is a square, then it is a rectangle,” we call the “a polygon is a square” the antecedent or the hypothesis, while “it is a rectangle” is called the consequent or conclusion.The figure above is an instance of the antecedent. The square in the figure is an instance for which the statement is true.
In the statement “if p is a prime, then p is an odd number” is another example of an if then statement. The number 17 is an instance for which the statement is true; 17 is prime and 17 is odd. However, 2 is prime, but it is not odd, so it is in an instance that makes the statement false. We call 2 a counterexample to this statement.
A counterexample is an exception to a proposed general rule. It is also a specific instance of the falsity of a generalization. In the example above, the generalization implies that all primes are odd; however, we have shown that this is not the case.
The Truth Tables
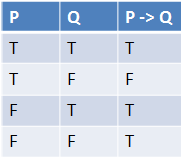
If then statements are of the form if P then Q, where P is the antecedent and Q is the consequent. In logic, the symbol 
- 17: P is true (17 is a prime), Q is true (it is odd) and the implication of the statement is true.
- 2: P is true (2 is prime), Q is false (2 is not odd) and as we have discussed above this makes the statement false.
- 25: P is false (25 is not prime) and Q is true (it is odd) and the statement is true.
- 8: P is false (8 is not prime) and Q is false (8 is not odd) and the implication is true.
The truth table below is derived from the list above. As we can observe, the statement is only false if P is true and Q is false.
Another Example
Let’s take the example above of a statement, say it is a dad’s promise to his son, that
If you pass the exam, then I’m going to buy you a tablet.
If P and Q are both true, son passes exam and dad buys a tablet. Promise is not broken (implication is true).
If P and Q are both false, son fails exam, dad doesn’t buy tablet (no hard feelings). Promise is not broken (implication is true).
If P is true and Q is false, son passes exam, dad doesn’t buy tablet (big problem), promise is broken (implication is false),
If P is false and Q is true, son fails exam, dad buys tablet (cool dad), promise is not broken (implication is true).
As we can see, this statement is consistent with the first example.