Introduction to Geometric Construction
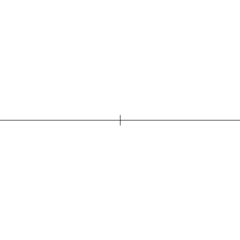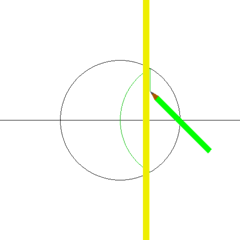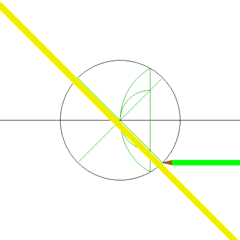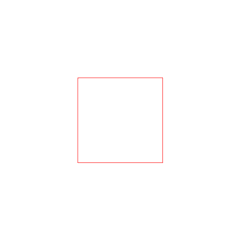
In Geometry, the term construction refers to a precise way of drawing using two tools, an unmarked straightedge and a compass. The straightedge is assumed to have an infinite length and has no markings. In constructions, these tools and only these tools must be used to construct lines, curves, and polygons. Shown below is an animation showing how to construct a square using compass and straightedge.
The Construction Rules
In construction, aside from the tools, there are specific rules to be followed. These rules are the following.
Point Rule: A point must either be given or be the intersection of figures that have been already constructed.
Straightedge Rule: A straightedge can draw the line AB through two points A and B.
Compass Rule: A compass can draw a circle with center at a point A containing a second point B.
Using compass and straightedge, it is possible to copy a segment by lifting the compass without movement (and therefore keeping the radius). With appropriate strategies, these two tools are enough for making complex constructions such as constructing a square shown in the animation above. Of course, constructions that are a lot more complicated than the animation above can be done.
Compass and straightedge construction play a great role in Euclidean Geometry. Euclid’s postulates, particularly the first three (see Elements) which is the foundation of Euclidean Geometry are principles of construction. In addition, three of the hardest problems of antiquity, namely squaring a circle, doubling a cube, and trisecting an angle are all construction problems.
If you want to learn about construction, Math Open Reference has an excellent collection of animated step by step compass and straightedge constructions. I suggest that you study these constructions and prove them.
****
Reference: Geometry (University of Chicago School Mathematics Project)
Image via Wikipedia