Mersenne Primes Under the Microscope
What are Mersenne Primes?
The recent discovery of the largest known prime number which is 17 million digits highlighted the importance of Mersenne primes. This newest prime number and the thirteen largest primes are all Mersenne primes. But what are Mersenne primes really and why are they important in finding the largest prime numbers?
If a prime number can be expressed in the form ,
an integer, then it is said to be a Mersenne prime. The name came from Marin Mersenne who studied them, a French monk and well-known mathematician in the 17th century.
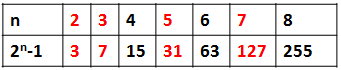
Many early mathematicians saw and conjectured that if n is a prime number, is prime. For instance, in the figure above, for
which are prime numbers, their corresponding
values are also prime numbers. However, this is not true in general since
is not prime.
Despite the counterexample for n = 11, is prime for
. These are
of the
prime numbers less than
. This fact gave mathematicians a hint that prime numbers can be found using the expression
where
is prime.
Finding Mersenne Primes Using Computers
Nowadays, with the use of powerful computers, it is easier to look for large prime numbers using a computer program The algorithm below maybe used to write a computer program (high school students who have knowledge in programming may want to try this) to look for large Mersenne primes.
- Choose a large prime
- Calculate
- Verify if
is prime.
To verify if the result in (3) is prime, the most basic technique would be to divide by all positive integers less than it. Note that there are less cumbersome strategies that would require shorter calculation time. For example, the square root of a number can be used to check if a large number is prime.
Despite the simplicity of the strategy above for finding Merenne primes, there are only 48 known Mersenne primes as of this writing. The reason is that computation of large numbers requires powerful computer hardware, an enormous amount of computer storage, and an ultra-fast memory. For instance, using a very powerful computer, it took 39 days of non-stop calculation to discover the largest prime number mentioned above. Aside from the actual calculation, verification was still done using different software and hardware.
About GIMPS
The calculation of the largest prime number mentioned above was performed by Great Internet Mersenne Prime Search (GIMPS), a non-profit organization dedicated to look for Mersenne Primes. GIMPS was founded by George Woltman in 1996. Since the start of the project until now, GIMPS has discovered 14 of the largest known prime numbers.