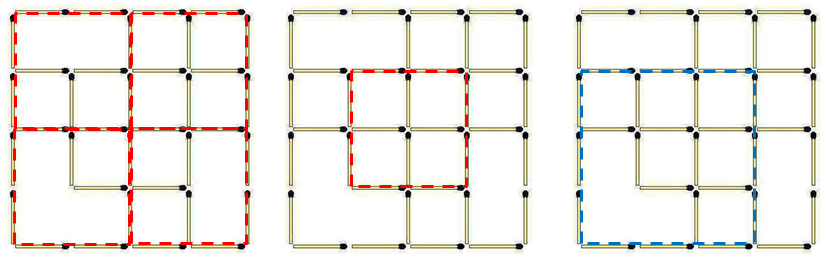
The Solution to the Matchstick and Square Puzzle
It’s been three months since I posted the Matchstick and Square puzzle. According to one of the comments, it’s already causing household arguments., so I think it’s high time that I post my solution. There is no key to the puzzle, I only found it on a Facebook Page.
Please check if my solution below is correct. 🙂
Solution
There are nine squares.
There are five squares.
There is one square.
There is one square.
Therefore, there 16 squares.