The Beauty of Mirrors and Symmetry

Symmetry is considered by many as a reflection of beauty and perfection. A symmetric object is an object where we can place a line such that the images on both sides of the line mirror each other.

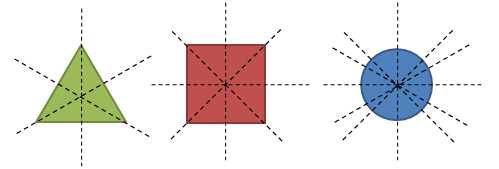
The geometric shapes in the first figure are symmetric. As shown, we can draw a line — in fact more than one line — to show symmetry. The equilateral triangle has three lines of symmetry, the square has four, and the circle has infinitely many.

We can see symmetry everywhere. Butterflies, lobsters, and some leaves, and flowers are symmetric. Many structures, buildings, and houses are symmetric. The human face and body are symmetric.  In fact, because of its ubiquity, people are trying to relate it to many things. For example, some claim that facial symmetry is an “indicator of freedom from disease and worthiness of mating.”

If someone claims that symmetry is a symbol of love, I would probably agree with him. In the 16th century, Shah Jahan, emperor of the Mughal Empire, was so grief-stricken that he spent about 32 million rupees for the construction of the Taj Mahal. The Taj Mahal was constructed as a mausoleum for his wife’s tomb. To date, it is still one of the most beautiful, symmetric structures ever created.

In school mathematics, we study symmetry in geometry and also along with transformation. In the coordinate plane, we know that if a figure with the y-axis as its line of symmetry, if this figure contains a point with coordinates , then its corresponding point has coordinates , a reflection over the y-axis. We have also learned that the reflected image is  congruent to its pre-image and that if we connect their corresponding points with a segment, the segment is perpendicular to the line of symmetry.