Latitudes, Longitudes and the Polar Coordinate System
In the early times, mathematicians and astronomers observed that the stars rotate about a point near the star now known as Polaris. This is one of the bases why some of them, particularly Copernicus, believed that the Earth spins on its axis and revolves around the sun.
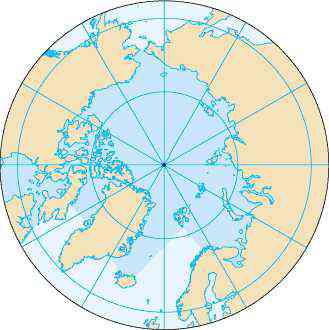
The longitude, the “vertical divisions” of Earth, meet at the North and the South Poles. With the addition of latitudes, the Earth’s “horizontal divisions,” a view of these lines from one of the poles is shown above. The longitudes appear as lines radiating from the pole (the center) and the latitudes as concentric circles. The largest circle is the equator.
If a reference line is drawn, say a horizontal line as shown in the second figure, any point on Earth from one of the poles to the equator can be determined by two coordinates: its distance from the pole and the angle of rotation about the pole from the horizontal line. This type of coordinate system is similar to the polar coordinate system.
In mathematics, the polar coordinate system is a 2-dimensional coordinate system where each point on the plane is described by its distance from a fixed point and an angle from a fixed direction. In the second figure, the distances of the two points are represented by the radii 
Some of the application of the polar coordinate systems are used for modeling circular and orbital motions. A slightly modified version of it is also used in navigation. Incoming sounds for microphones from a particular direction can also be modeled by polar curves.