Math Trick 1: Squaring Numbers Ending in 5
Math tricks and mental math shortcuts are used to perform speedy calculations. Many of us know at least a trick or two because they are easy to remember and handy to use. But why or how do these tricks work?
This is the first of a series of posts that will discuss math tricks and mental math shortcuts. Aside from the algorithm that will be taught in this series that will benefit everyone, we will also investigate why they work.
The Trick: Squaring Numbers Ending in 5
Squaring numbers ending in 5 is probably the most popular among the math tricks and mental shortcuts. Below is the algorithm of the trick.
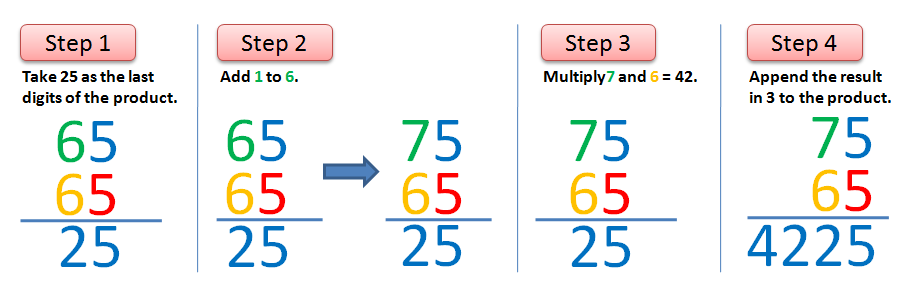
Steps
- Take 25 as the last two digits of the product of the factors.
- Add 1 to the tens digit of one of the factors.
- Take away 5 from both the factors, and multiply the remaining numbers.
- Append the product in the third step to the left of the result in the first step.
Observe that in doing the algorithm above, the number on the right hand side of the product of the squared numbers is always 25.
The algorithm presented above will work on all 2-digit numbers ending in 5. You might want to try several numbers for verification.
Extension
What most people do not know about this trick is that it can be extended to larger numbers. Although it is more difficult to compute mentally as the numbers become larger, it is quite surprising that the trick works. Let us try a 3-digit number 335.
Steps
- Take 25 as the last two digits of the product of the factors.
- Add 1 to the tens digit of one of the factors (33 + 1 = 34).
- Take away 5 from both the factors, and multiply the remaining numbers (34 x 33 = 1122).
- Append the product in the third step to the left of the result in the first step. This gives us 112225
If you check, 335 x 335, the answer is 112225.
What Really Happened
Any integer ending in 5 can be written as 10k + 5, where k is any non-negative integer. In the examples above, 65 = 10(6) + 5 and 335 is 10(33) + 5. With this fact, let us examine what happened in the math tricks above.
In the first example, we square the ones digit. Second, we add 10 to one of the tens digits. And third, we multiply the ten’s digits. If we express this in the form 10(6) + 5, we did the following:
Step 1
What we did: We took 25 as the last digit of the product of the squared numbers.
What really happened: We multiplied 5 x 5 = 25
Step 2
What we did: We added 1 to 6, 6 + 1 = 7.
What really happened: Since 6 and 1 are tens digits, we really added 60 + 10 = 70.
Step 3
What we did: We multiplied 6 x 7 = 42. .
What really happened: Again, since both are tens digits, we actually multiplied 60 x 70 = 4200.
Step 4
What we did: We appended 42 to the left of 25.
What really happened: 4200 was added 25 which results to 4225.
Why the Trick Works
Now why do taking 25 as the last digit, then adding 1 to the tens digit, and then multiplying the numbers after discarding 5 work? Let us examine the algebraic properties of the process.
The Generalized Trick
The number we squared is in the form 10k + 5. We took 25 as the last two digits of the product, and multiplied 10k and 10(k+1). Remember, we added 1 to the tens digit of k. Then we multiplied and added to 25. The final result will be 10k[10(k + 1)] + 25 = 10k(10k + 10) = 100k2 + 100k+ 25.
Generalized Conventional Calculation
Performing the conventional computation (without tricks) (10k + 5) (10k + 5) = 100k2 + 50k + 50k + 25 = 100k2 + 100k + 25.
As we can see both the conventional computation and the calculation using the trick have the same result. Therefore, we have shown that the math trick will always work .