The 3 Ancient Construction Problems

General Education, High School Geometry, High School Mathematics

Problems about construction using compass and straightedge preoccupied mathematicians for 2000 years. The first three postulates of Euclid’s Elements (300 BC) involve constructions and the first proposition was about the construction of an equilateral triangle. Constructions of other regular polygons were solved, but the heptadecagon (17-gon) proved to be difficult. It was only solved by Carl Friedrich Gauss in 1796 when he was just 19 (see the following animation).

17-gon construction

Aside from the heptadecagon problem and other construction problems, numerous mathematicians attempted to solve the three most difficult ancient construction problems: trisection of any given angle, duplication of a cube, and squaring the circle.

Trisection of Angle

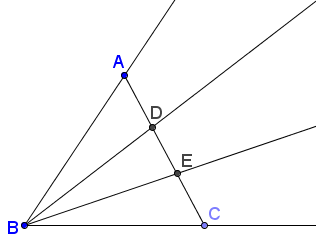
The trisection angle problem states that given an angle ABC, use the compass and straightedge to construct rays BD and BE so that

\angle ABD \cong \angle DBE \cong \angle EBC.

At first glance, the solution seems obvious. For instance, take AB = AC. In connecting B and C, we can show that angle \angle ABD \cong \angle EBC but these angles are not congruent to \angle DBE.

trisecting an angle

Mathematicians tried to make this construction, but it was proved by Pierre Wantzel (1837) to be impossible.

Doubling the Cube

The cube problem was tied to Greek mythology. According to myth, a large number of people were dying at Delos (a city in Greece) so the Delians consulted the oracle at Delphi. The oracle told them that Apollo was displeased and wanted his cubical altar to be twice as large of the original one. The poor Greeks built another altar doubling each length of the altar only to find out that the volume was increased eight times. Hence, mathematicians search for ways in doubling a cube (its volume).

Doubling a cube is another construction problem which means that the only permitted instruments are the compass and straightedge. If Algebra was invented during that time, the Greeks would have lived longer since if the volume of the first cube is a^3, then the required volume is 2a^3. If we let

b^3 = 2a^3,

then they needed the edge length of the altar to be b = a\sqrt[3] {2}.

It was also proved in the modern time that this problem is impossible to solve.

Squaring the Circle

Squaring the circle means given a circle, we want to construct a square of the same area using only compass and straightedge. It was proved by Ferdinand  von Lindemann in 1882 that the construction was impossible by proving that \pi is a transcendental number.

Today, the phrase “squaring the circle” means “to do the impossible.”

Leave a comment , , , , , ,

Leave a Reply